1 Vypočtěte:
1.1
1.2
2
2.1 Vypočtěte, o kolik litrů se liší čtvrtina z 24 litrů a třetina z 12 litrů.
2.2
Vynásobením dvou kladných celých čísel jsme získali součin 180. Jedno z těchto dvou čísel zvětšíme dvakrát a jedno zmenšíme šestkrát.
Určete, jaký součin získáme vynásobením obou změněných čísel.
VÝCHOZÍ TEXT K ÚLOZE 3
V rotě je jeden kapitán a má pod sebou 4 poručíky. Každý poručík má pod sebou 3 své četaře a každý četař má pod sebou 10 svých vojínů. (Další osoby v rotě nejsou.) Kapitán se rozhodl svolat celou rotu k nástupu. Rozkaz k nástupu se předával tak, že kapitán vydal rozkaz všem poručíkům, z nichž každý vydal tento rozkaz svým četařům a každý četař jej vydal svým vojínům. Poté celá rota nastoupila.
3 Vypočtěte,
3.1 kolik je v rotě vojínů,
3.2 kolik osob v rotě vydalo rozkaz k nástupu,
3.3 kolik osob v rotě dostalo rozkaz k nástupu.
VÝCHOZÍ TEXT K ÚLOZE 4
Jana koupila v papírnictví několik stejných linkovaných sešitů, několik stejných čtverečkovaných sešitů a několik stejných kružítek.
4
4.1 Jana koupila celkem 36 sešitů, přičemž linkovaných koupila třikrát více než čtverečkovaných.
Vypočtěte, kolik linkovaných sešitů koupila.
4.2 Dva linkované sešity a dva čtverečkované sešity stojí dohromady 180 korun.
Dva čtverečkované sešity stojí stejně jako tři linkované.
Vypočtěte, kolik korun stojí jeden čtverečkovaný sešit.
4.3 K nákupu šesti kružítek chybělo Janě 160 korun, proto koupila jen čtyři kružítka a zbylo jí 100 korun.
Vypočtěte, kolik korun zaplatila za 4 kružítka.
VÝCHOZÍ TEXT K ÚLOZE 5
Pro děti klubu SEN se letos otevřel pouze sportovní, divadelní a robotický kroužek. Každé dítě klubu SEN navštěvuje alespoň jeden z těchto tří kroužků – 3 děti navštěvují všechny tři kroužky, 8 dětí navštěvuje právě dva kroužky a ostatní děti jediný kroužek. Sportovní kroužek navštěvuje 14 dětí, divadelní 12 dětí a robotický 6 dětí.
5 Vypočtěte,
5.1 kolik dětí klubu SEN navštěvuje pouze jeden kroužek,
5.2 kolik dětí je v klubu SEN.
VÝCHOZÍ TEXT K ÚLOZE 6
Na odměny pro tři nejlepší soutěžící byla připravena finanční částka v korunách. První soutěžící získal polovinu této částky. Druhý soutěžící dostal 300 korun. Třetí soutěžící získal zbytek připravené částky, což bylo třikrát méně korun, než získal první soutěžící.
6 Vypočtěte,
6.1 kolikrát více korun dostal druhý soutěžící než třetí soutěžící,
6.2 kolik korun bylo celkem připraveno na odměny
7
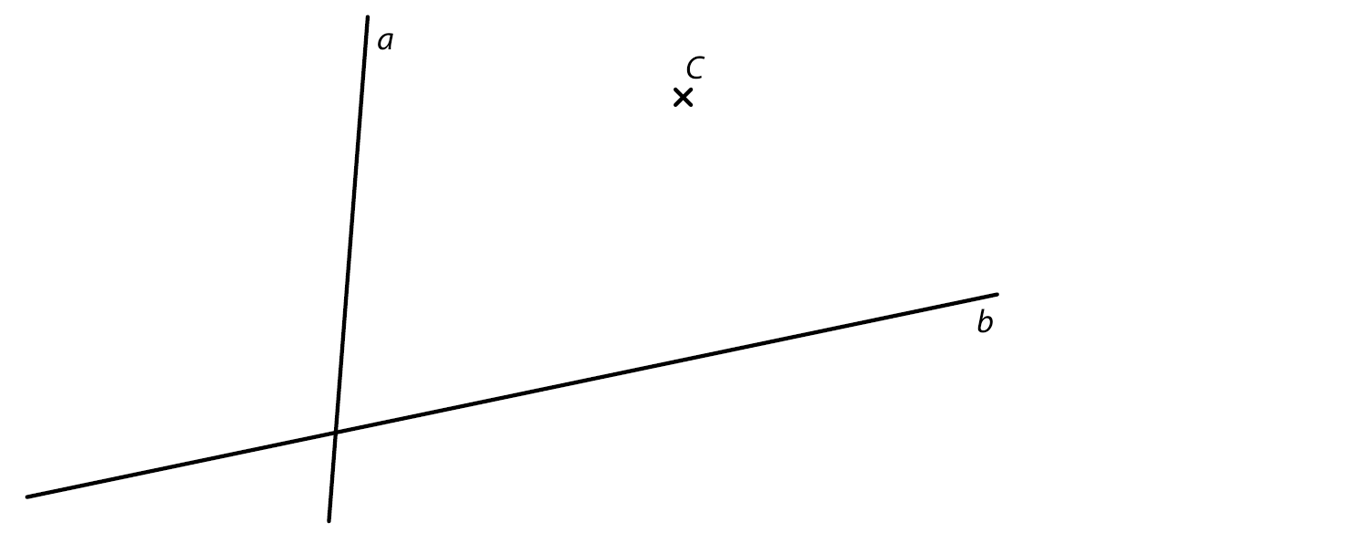
7.1 Bod C je vrchol trojúhelníku ABC.
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7.1
V rovině leží bod C a přímky a, b.
Na přímce a leží vrchol A a na přímce b vrchol B tohoto trojúhelníku.
Strana AC trojúhelníku ABC je rovnoběžná s přímkou b.
Strany AB a AC mají stejnou délku.
Sestrojte vrcholy A, B trojúhelníku ABC, označte je písmeny a trojúhelník narýsujte. Najděte všechna řešení.
V záznamovém archu obtáhněte vše propisovací tužkou (čáry i písmena).
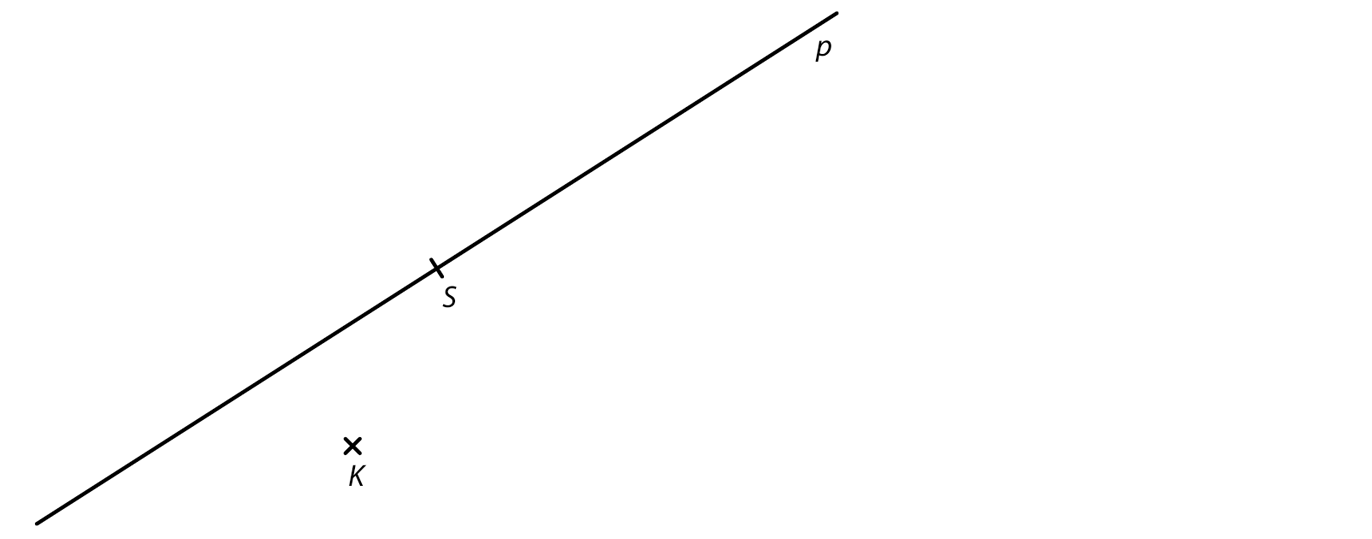
7.2 Bod K je vrchol obdélníku KLMN.
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7.2
V rovině leží body K, S a přímka p procházející bodem S.
Bod S je střed strany KL tohoto obdélníku.
Přímka p prochází středem S strany KL a středem ještě jedné strany obdélníku KLMN.
Sestrojte vrcholy L, M, N obdélníku KLMN, označte je písmeny a obdélník narýsujte. Najděte všechna řešení.
V záznamovém archu obtáhněte vše propisovací tužkou(čáry i písmena).
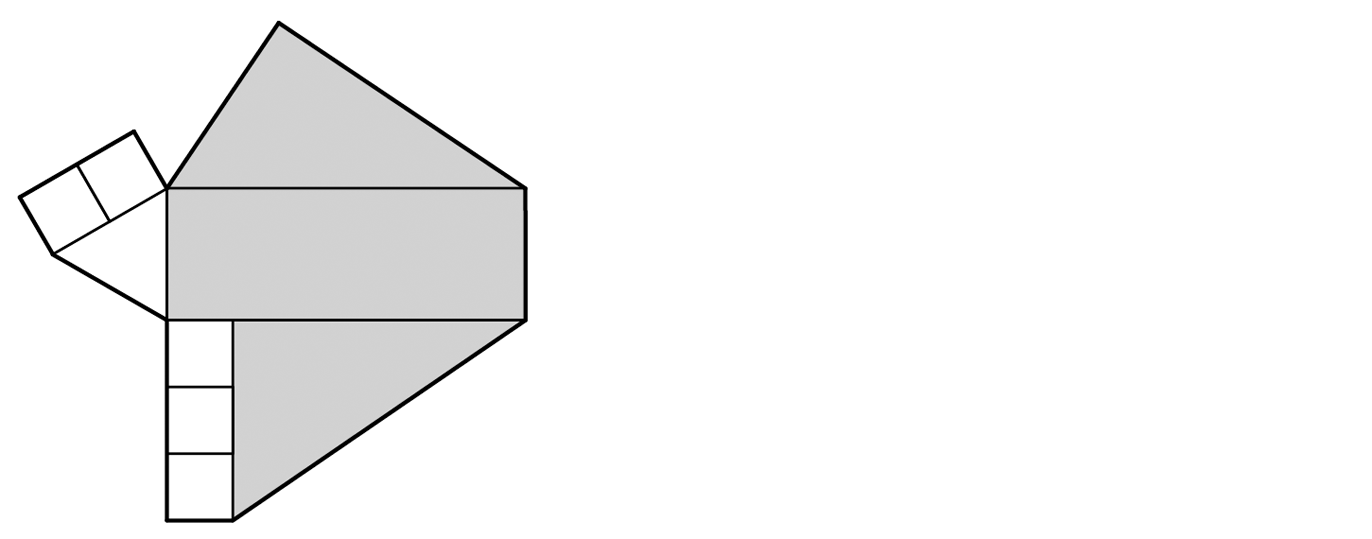
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8
Desetiúhelník na obrázku se skládá z jednoho rovnostranného trojúhelníku, pěti stejných čtverců, jednoho šedého obdélníku a dvou stejných šedých trojúhelníků. Nejkratší strana desetiúhelníku měří 4 cm, nejdelší 20 cm.
8 Rozhodněte o každém z následujících tvrzení (8.1–8.3), zda je pravdivé (A), či nikoli (N).
8.1 Obvod rovnostranného trojúhelníku je 12 cm.
8.2 Obvod šedého obdélníku je 56 cm.
8.3 Obvod šedého trojúhelníku je větší než 50 cm.
VÝCHOZÍ TEXT K ÚLOZE 9
Maminka koupila v cukrárně tři různé zákusky. První zákusek stál 72 korun. Druhý zákusek byl o čtvrtinu levnější než první. Cena třetího zákusku byla třetinou celkové ceny všech tří zákusků.
9 O kolik korun byl třetí zákusek dražší než druhý?
o méně než 12 korun
o 12 korun
o 15 korun
o 18 korun
o více než 18 korun
VÝCHOZÍ TEXT K ÚLOZE 10
V kasičce je celkem 78 mincí – některé jsou pětikorunové a zbývající desetikorunové. Hodnota všech pětikorunových mincí v kasičce je stejná jako hodnota všech desetikorunových mincí v kasičce.
10 Jaká je hodnota všech mincí v kasičce?
390 korun
520 korun
585 korun
780 korun
jiná hodnota
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOHÁM 11–12
Stavebnice obsahuje samé stejné dílky. Každý dílek má tvar kvádru s rozměry 6 cm, 4 cm a 4 cm.
11 Kolik dílků stavebnice je třeba ke složení kvádru s rozměry 8 cm, 12 cm a 16 cm?
méně než 12 dílků
12 dílků
16 dílků
32 dílků
více než 32 dílků
12 Kolik dílků stavebnice je třeba ke složení nejmenší možné krychle?
méně než 6 dílků
6 dílků
12 dílků
18 dílků
více než 24 dílků
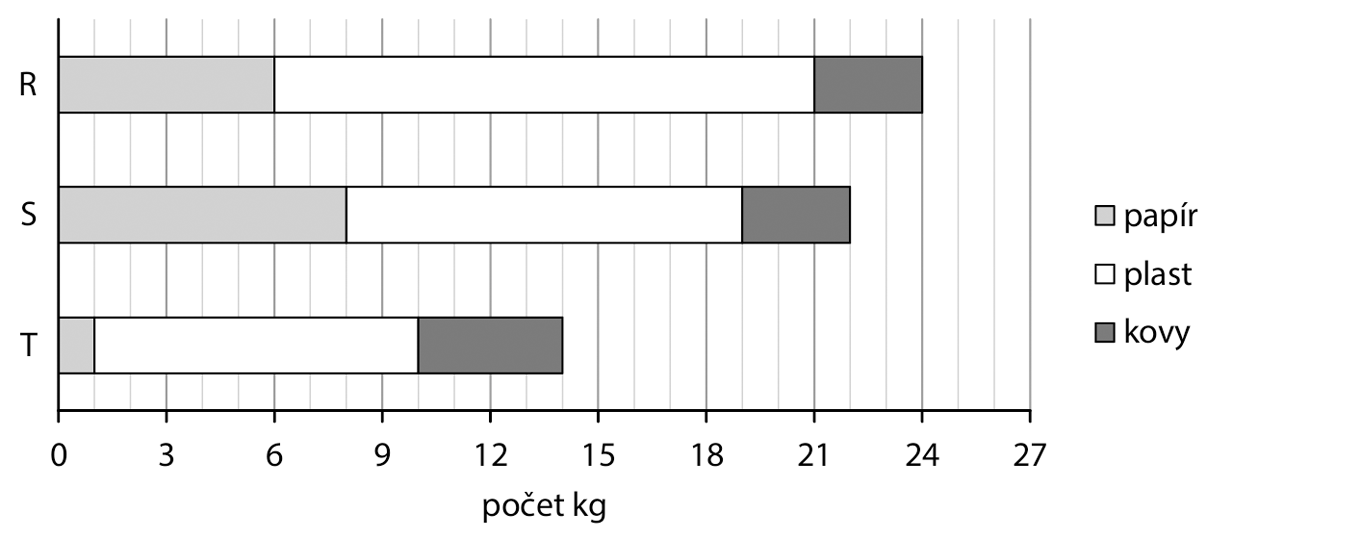
VÝCHOZÍ TEXT A GRAF K ÚLOZE 13
Graf udává, kolik kg odpadu vytřídily tři skautské oddíly R, S a T.
13 Do každé neúplné věty (13.1–13.3) doplňte na vynechané místo (……………) chybějící část (A–F) tak, aby vzniklo pravdivé tvrzení.
13.1 Oddíl R vytřídil …………… méně kg papíru než oddíl S.
13.2 Oddíly S a T dohromady vytřídily …………… více kg plastu než oddíl R.
13.3 Všechny tři oddíly dohromady vytřídily …………… více kg papíru než kovů.
o šestinu
o pětinu
o čtvrtinu
o třetinu
o polovinu
dvakrát
VÝCHOZÍ TEXT A OBRÁZKY K ÚLOZE 14
Ze stejně velkých světlých a tmavých čtverečků tvoříme obrazce tvaru čtverce nebo obdélníku. Základní obrazec je tvořen jednou nebo více řadami světlých čtverečků.
Z každého základního obrazce vytvoříme rozšířený obrazec tak, že přidáme nahoru jednu řadu tmavých čtverečků a pak vlevo i vpravo po jednom sloupci tmavých čtverečků.
14
14.1 Ze základního obrazce, který má 5 řad, vytvoříme rozšířený obrazec přidáním 30 tmavých čtverečků.
Určete počet sloupců v základním obrazci.
14.2 Rozšířený obrazec má 3 řady a tvoří jej stejný počet tmavých a světlých čtverečků.
Určete počet sloupců v rozšířeném obrazci.
14.3 Můžeme najít mnoho rozšířených obrazců s 50 tmavými čtverečky.
Určete počet všech těchto rozšířených obrazců.