1 Vypočtěte:

1.1

5⋅115+(232+21⋅8):(5+60:3)=5 \cdot 115 + (232 + 21 \cdot 8) : (5 + 60 : 3) =

1.2

(128+16:4−32):(30+5⋅13−9⋅5)−1=(128 + 16:4 - 32):(30+5 \cdot 13-9\cdot5) - 1 =

2 Najděte a napište jednu číslici, kterou lze nahradit všechny hvězdičky tak, aby byl výpočet správný.

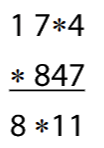
alt text

Do záznamového archu uveďte pouze chybějící číslici.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 3

V součtovém trojúhelníku platí, že součet dvou čísel, které jsou v řádku vedle sebe, je vždy zapsán o řádek níže do rámečku, který s těmito oběma čísly sousedí.

Například:

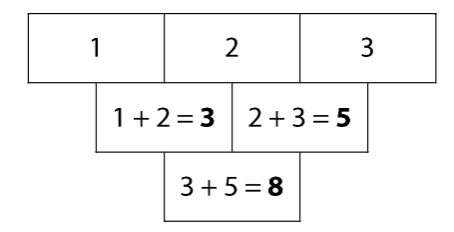
alt text

Mějme součtový trojúhelník:

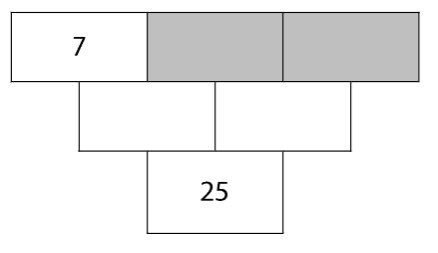
alt text

3 Do obou šedých polí patří stejné číslo.

Jaké číslo musí být v obou šedých polích?

Do záznamového archu uveďte pouze chybějící číslo, které patří do šedých polí.

4 Řešte slovní úlohy.

4.1 Zuzanka koupila dárek a krabičku, do které ho chtěla zabalit. Celková cena za dárek i krabičku byla 84 Kč. Dárek byl o 72 Kč dražší než krabička.

Kolikrát je dárek dražší než krabička?

4.2 Lukáš má svůj účet, na který mu maminka pravidelně posílá kapesné, on sám si tam ukladá všechny své našetřené peníze. K narozeninám dostal od babičky 500 Kč. Ty použil na koupi knížky, která stála 186 Kč, a zbylé peníze si uložil na účet. Poté mu na účet maminka poslala kapesné 150 Kč a Lukáš druhý den z účtu vybral 263 Kč na dárek pro tatínka. Na účtu mu pak zbylo 470 Kč.

Kolik peněz měl Lukáš na účtu před narozeninami, pokud k jiným pohybům na účtu nedošlo?

4.3 U úterý ráno měli v obchodě bednu plnou jablek. Dopoledne z jablek v této bedně prodali jednu pětinu a do konce dne ještě 20 kusů. Poté jim na druhý den v bedně zůstaly dvě pětiny jablek.

Kolik jablek bylo v úterý ráno v plné bedně?

5 Doplňte do rámečku takové číslo, aby platila rovnost.

5.1 1 hodina + 20 minut = |???| sekund

5.2 12\frac12 metru + |???| milimetrů = 1 metr - 26 centimetrů

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 6

Na číselné ose je vyznačeno 12 shodných úseků, čísla 44 a 110 a neznámá čísla X a Y.

alt text

6

6.1 Určete neznámá čísla X a Y.

6.2 Na číselné ose vyznačte nulu.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7

V rovině leží přímka p a mimo ni body A a S. alt text

7 Bod A je vrcho obdélníku ABCD. Bod S je střed strany AB tohoto obdélníku. Na přímce p leží bod Q, střed některé ze sousedních stran strany AB tohoto obdélníku.

7.1 Sestrojte vrchol B.

7.2 Na přímce p najděte a popište střed Q delší strany obdelníku, sestrojte a popište vrcholy C a D a obdélník ABCD narýsujte. Najděte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

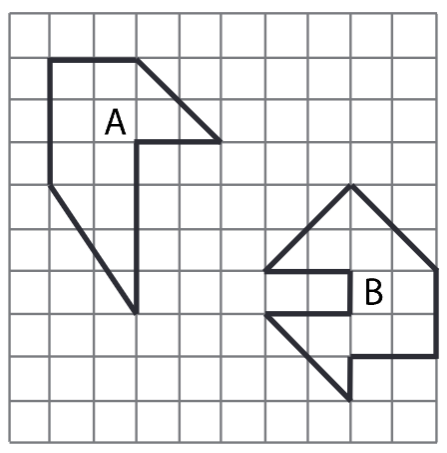
Ve čtercové síti jsou nakresleny dva obrazce A a B, jejichž vrcholy leží v mřížových bodech. Každý čtvereček čtvercové sítě má stranu délky 1 cm a obsah 1 cm 2. alt text

8 Rozhodněte o každém následujích tvrzení (8.1-8.3), zda je pravdivé (A), či nikoliv (N).

8.1 Obsahy obou obrazců si jsou rovny.

8.2 Obsah obrazce A je 11 cm2.

8.3 Obvod obrazce B je 16 cm..

9 Tereza a její kamarádka Nikola píší novoroční přání. Všechna přání mají stejný text a každá z dívek píše stálou rychlostí. Tereza za každých 5 minut napíše 14 novoročenek, zatímco Nikola 10.

Za jak dlouho společně napíší 120 novoročních přání?

A)

za 24 minut

B)

za 25 minut

C)

za 30 minut

D)

za 32 minut

E)

za jiný počet minut

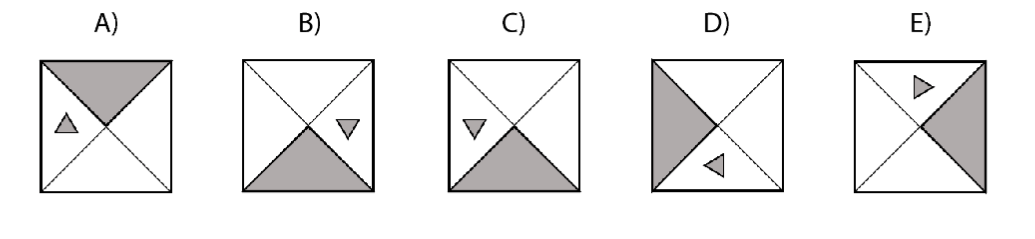
VÝCHOZÍ OBRÁZEK K ÚLOZE 10

alt text

10 Který z uvedených obrázků (A-E) logicky nepatří mezi ostatní?

A)
B)
C)
D)
E)

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11

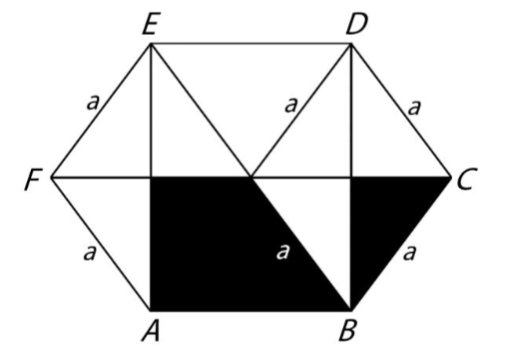
Máme šestiúhelník ABCDEF, který lze úsečkami AD, BE a CF rozdělit na šest shodných rovnoramenných trojúhelníků. Body A,B,D a E leží ve vrcholech obdélníku. Obsah tmavé části šestiúhelníku je 112 cm2. alt text

11 V je obsah bílé části šestiúhelníku?

A)

28 cm2

B)

112 cm2

C)

196 cm2

D)

224 cm2

E)

jiný obsah

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12

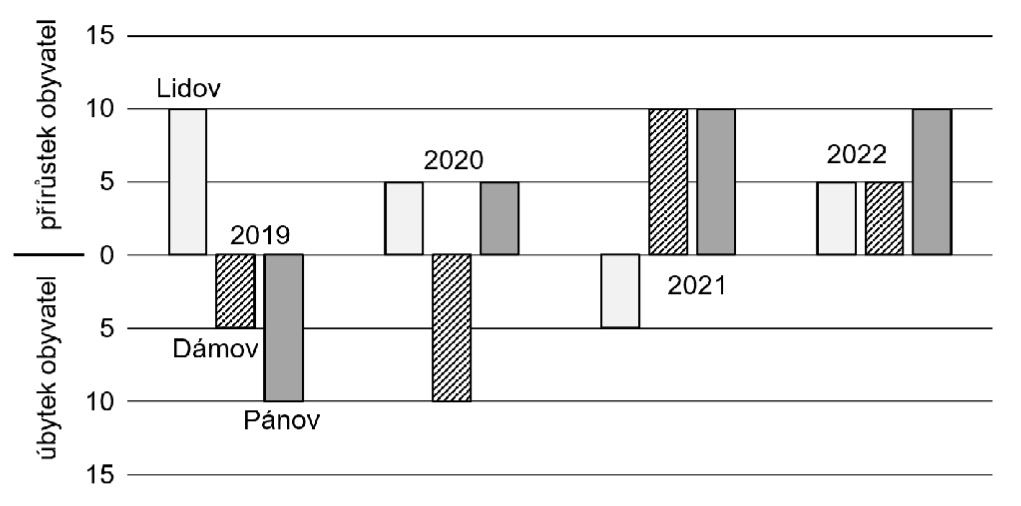
Graf znározňuje přírůstek a úbytek obyvatel v obcíh Lidov, Dámov a Pánov v letech 2019-2022. alt text

12

12.1 Jak se změnil počet obyvatel v Pánově během roku 2021?

A)

Ubylo 5 obyvatel.

B)

Ubylo 10 obyvatel.

C)

Počet obyvatel se nezměnil.

D)

Přibylo 5 obyvatel.

E)

Přibylo 10 obyvatel.

12.2 Jestliže na počátku čtyřletého období 1.ledna 2019 žilo v Lidově 300 obyvatel, kolik obyvatel žilo ve stejné obci po třech letech 31.prosince 2021?

A)

290

B)

295

C)

305

D)

310

E)

315

12.3 Jak se změnil počet obyvatel v Dámově za všechny čtyři roky dohromady?

A)

Ubylo 5 obyvatel.

B)

Počet obyvatel se nezměnil.

C)

Přibylo 5 obyvatel.

D)

Přibylo 15 obyvatel.

E)

Jiný výsledek.

VÝCHOZÍ TEXT K ÚLOZE 13

Pan Josef jel autem z Heraltic do Třebíče stálou rychlostí a cesta mu trvala 24 minut. V 7:08 byl v jedné třetině cesty. V polovině cesty projel přes železniční přejezd.

13 Ke každé podúloze (13.1-13.3) přiřaďte správný výsledek (A-F)

13.1 V kolik hodin pan Josef vyjel?

13.2 V kolik hodin přejel pan Josef železniční přejezd?

13.3 V kolik hodin by pan Josef přijel, kdyby vyjel o 6 minut později?

A)

7:30

B)

7:24

C)

7:12

D)

7:08

E)

7:00

F)

6:52

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

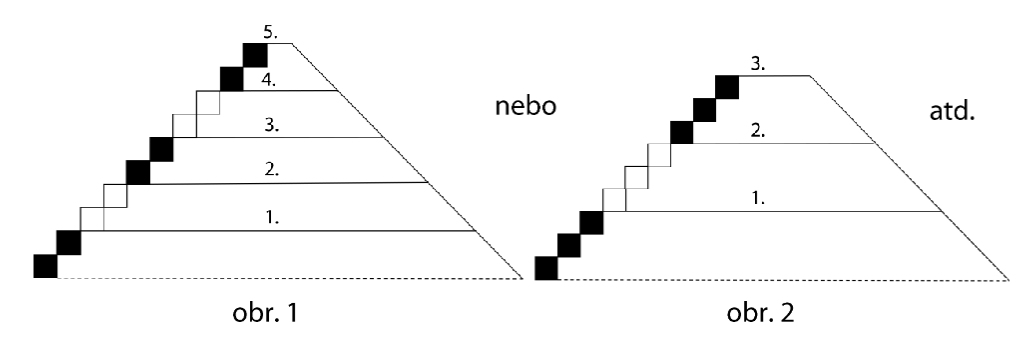
Pyramida postavená z kostek stavebnice může mít libovolný počet pater. Každé patro pyramidy má stejnou výšku. Do prvního, druhého a každého dalšího patra vede vždy stejný počet schodů. Zdola do prvního patra vedou vždy černé schody, do druhého patra bílé schody a takto se rovněž ve vyšších patrech obě tyto barvy schodů pravidelně střídají.

Např. na obr. 1 má pyramida 6 černých schodů a 4 bílé schody, na obr.2 má pyramida 6 černých schodů a 3 bílé schody. Další pyramidy vytváříme v souladu s výchozím textem. alt text

14

14.1 Pyramida s 8 patry má celkem 48 černých schodů.

Kolik schodů vede do prvního patra?

14.2 Pyramida se 7 patry má celkem 84 bílých schodů.

Jaký je celkový počet schodů v pyramidě?

14.3 V pyramidě s 90 schody má 27.schod stejnou barvu jako 30.schod, ale jinou barvu než 33.schod.

Jaký je největší možný počet pater v této pyramidě?