1 Vypočítejte.

1.1 Máme čísla A a B. A = 1,6, B = -1,2.

Kolikrát je součet A + B menší než rozdíl A-B?

1.2 Napište desetinné číslo, které je o 0,093 menší než 78\frac{7}{8}.

2 Vypočítejte a výsledek zapište zlomkem v základním tvaru.

Do záznamového archu uveďte u obou podúloh celý postup řešení.

2.1

(58−16):11124⋅78=\frac{\left(\frac58 - \frac16\right):\frac{11}{12}}{4\cdot\frac78}=

2.2

2,5−78⋅45−2718:159=2,5-\frac78\cdot\frac45-\frac{27}{18}:\frac{15}{9}=

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 3

Na číselné ose se stejně velkými dílky jsou označeny obrazy čísel 1,4 a 5,6 a obrazy neznámých čísel A,B,C.

alt text

3

3.1 Zapište hodnotu čísla C.

3.2 Zapište, kolikrát je číslo B větší než číslo 1,4.

3.3 Vypočítejte rozdíl A - B.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 4

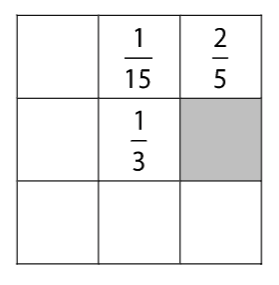
Na obrázku je částečně vyplněný tzv. magický čtverec, pro který platí: součet všech tří zlomků je stejný v každém řádku, sloupci a v každé úhlopříčce a rovná se 1.

alt text

4 Jaký zlomek se nachází v šedém poli?

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 5

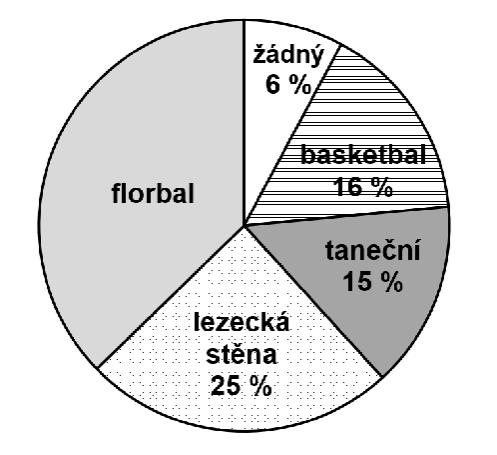
V kruhovém diagramu je vyznačeno, kolik dětí z jedné základní školy navštěvuje jednotlivé kroužky a kolik dětí této školy nechodí do žádného kroužku. Víme, že na florbal chodí 114 dětí a každé dítě navštěvuje nejvýše jeden kroužek.

alt text

5

5.1 Kolik dětí navštěvuje nějaký kroužek?

5.2 Kolik dětí chodí na basketbal?

6 Počet sportovců na závodech byl více než 1 a zároveň méně než 90. Pořadatel chtěl sportovce seřadit do slavnostního průvodu, ale ať je rozděloval do dvojic, trojic, čtveřic nebo pětic, vždy mu jeden sprotovec zbyl.

Kolik sportovců se sešlo na závodech?

7 V útulku mají 5 štěňat. Krmení zvířat probíhá každý den odpoledne. 2. dubna ráno otevřeli 10kg balení granulí pro psy, které těmto pěti štěňatům dohromady vystačí na 16 dní. 8.dubna ráno bylo do útulku přivezeno 1 štěně a 2 dospělí psi. Víme, že každý dospělý pes sní za den dvojnásobek dávky určené pro štěně.

Kolikátého dubna byli naposledy psi a štěňata krmeni granulemi z tohoto balení?

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

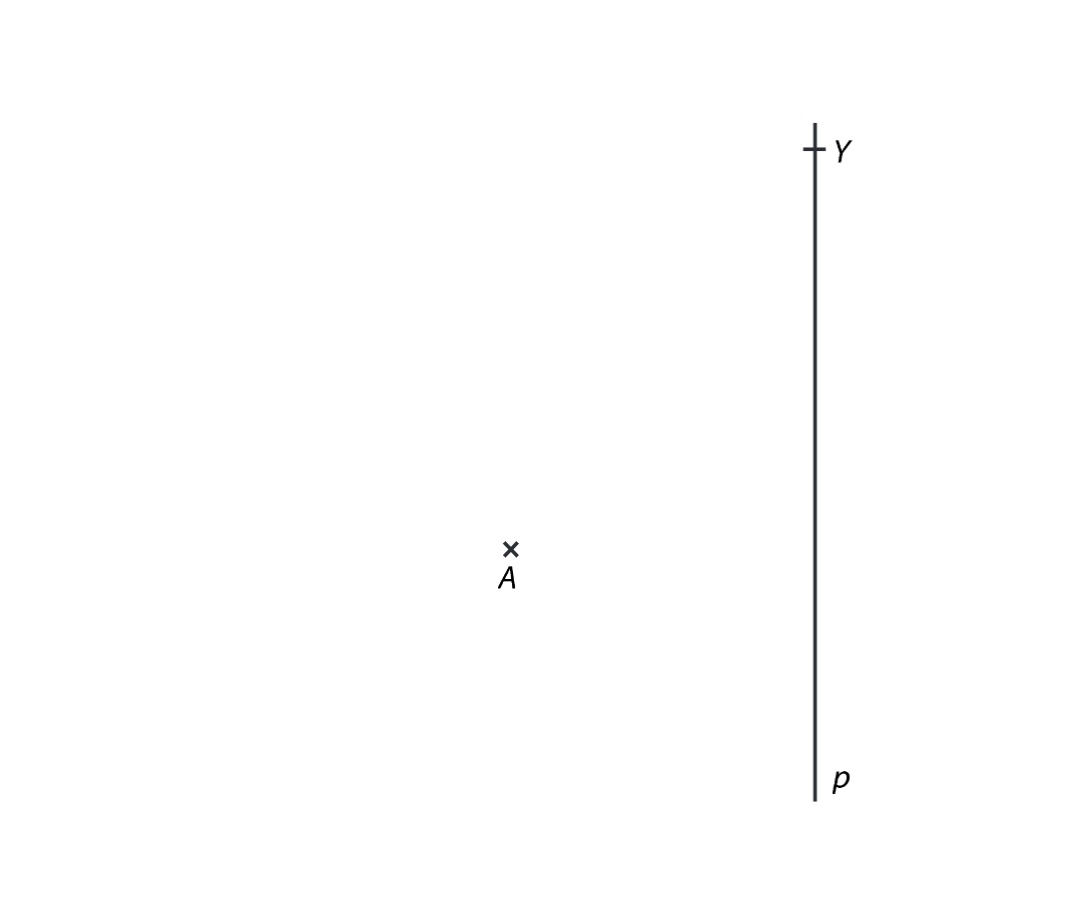
Je dána přímka p a bod A, který neleží na přímce p.

alt text

8 Sestrojte pravoúhlý lichoběžník ABCD, pokud platí:

Rameno kolmé k základně AB leží na přímce p. Strana AB lichoběžníku ABCD má stejnou délku jako strana AD. Strana AB je dvakrát delší než strana BC. Bod C leží na polopřímce BY.

Najděte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

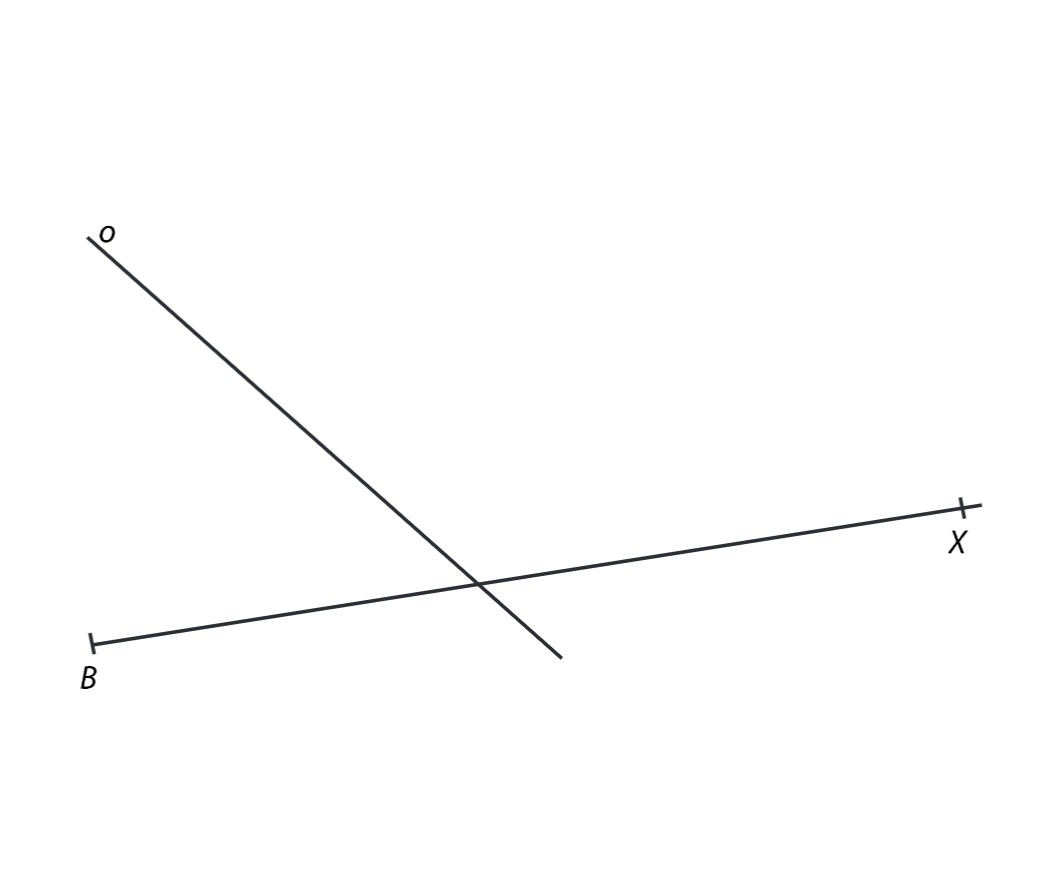
V rovině leží polopřímka BX a přímka o.

alt text

9 Bod B je vrchol rovnoramenného trojúhelníku ABC. Přímka o je osou strany BC trojúhelníku. Bod A leží na polopřímce BX.

Sestrojte rovnoramenný trojúhelník ABC se základnou AC.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT K ÚLOZE 10

Na letním táboře jsou kromě dětí také instruktoři, vedoucí, kuchařky a jeden zdravotník. Počet zdravotníků a počet kuchařek je v poměru 1:4, počet kuchařek a vedoucích 1:2, počet vedoucích a instruktorů 1:2 a počet instruktorů a dětí 1:4. Všichni jsou ubytováni ve 47 stanech. Zdravotník je ve stanu sám, ostatní jsou ubytováni po dvou.

10 Rozhodněte o každém následujích tvrzení (8.1-8.3), zda je pravdivé (A), či nikoliv (N).

10.1 Na táboře je dohromady 22 vedoucích a instruktorů.

10.2 Instruktorů je 4krát více než kuchařek.

10.3 Na táboře je celkem 64 dětí.

11 V ohradě probíhali králici a slepice. Králíků bylo o 5 méně než slepic. Králíci a slepice měli dohromady 106 nohou a 37 hlav.

Kolik bylo v ohradě slepic?

A)

16

B)

18

C)

19

D)

20

E)

21

12 Charitativní závod startoval ve 14:00 (14 hodin). Závodit se mohlo pěšky nebo s využitím libovolného dopravního prostředku. Jana se rozhodla pro chůzi a šla rychlostí 4 kilometry za hodinu, Petra jela na kolečkových bruslích, Roman je na kole a Adam běžel. Roman byl pěkrát rychlejší než Jana a v cíli byl ve 14:30. Adamův běh byl třikrát rychlejší než chůze Jany, ale 40 minut po startu se Adam zranil a zbytek závodu absolvoval chůzí stejnou rychlostí jako Dana. Do cíle přišel 5 minut před Petrou.

V kolik hodin se dostal do cíle Adam?

A)

14:30

B)

14:45

C)

15:00

D)

15:10

E)

15:15

13 Kolikrát je obsah obdelníku o straně a = 36 cm a straně b = 12cm větší než obsah čtverce se stranou délky 6 cm?

A)

3krát

B)

6krát

C)

7,5krát

D)

12krát

E)

12,5krát

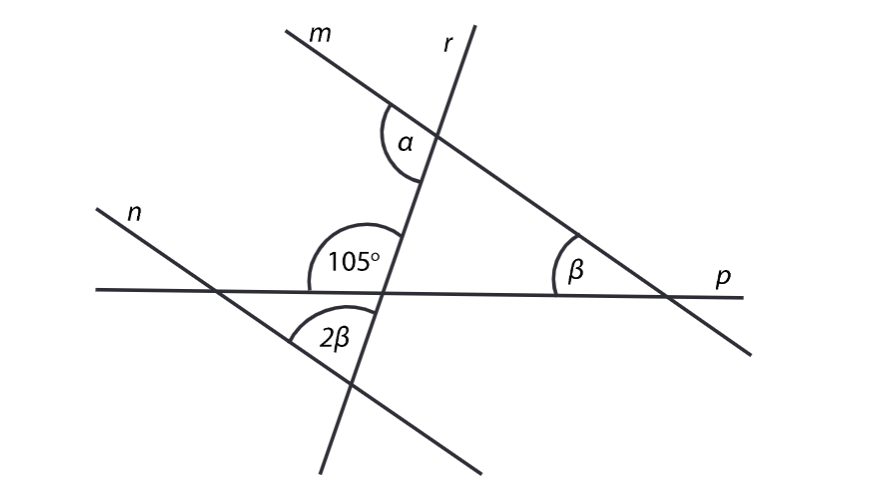
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

Přímky m,n jsou rovnoběžné. alt text

14 Jaká je velikost úhlu α\alpha?

A)

145°

B)

110°

C)

105°

D)

75°

E)

35°

15 Přiřaďte ke každé úloze (15.1-15.3) odpovídající výsledek (A-F)

15.1 Koupaliště během letošního léta navštívilo 680 návštěvníků, což je 80 % všech návštěvníků za celý minulý rok.

Kolik návštěvníků přišlo na koupaliště v loňském roce?

15.2 S cestovní kanceláří vycestovalo v červnu 330 klientů, což bylo o 40 % méně než v měsíci červenci.

Kolik klientů vycestovalo s cestovní kanceláří v červenci?

15.3 Na mapě s měřítkem 1:3 000 je vyznačen čtvercový pozemek o straně 15 cm.

Jaká je skutečná délka strany tohoto pozemku v metrech?

A)

450

B)

550

C)

650

D)

750

E)

850

F)

jiný výsledek

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16

Hranol o výšce 15 cm se skládá ze dvou shodných kvádrů s obdelníkovou podstavou a jednoho kvádru se čtvercovou podstavou. Podstava hranolu i s rozměry je na obrázku. alt text

16

16.1 Vypočítejte povrch tělesa.

Výsledek uveďte v cm2.

16.2 Vypočítejte objem tělesa.

Výsledek uveďte v cm3.