VÝCHOZÍ TEXT K ÚLOZE 1

Celý film trvá 1 hodinu. Doba, která ještě zbývá do konce filmu, je polovinou doby, která již uplynula od začátku filmu.

1 Vypočtěte, kolik minut zbývá do konce filmu.

2

2.1

Vnitřní objem sudu je 15krát větší než objem kbelíku.
Objem kbelíku je 5krát větší než objem konvičky.
Ze sudu plného vody jsme třetinu vody odebrali, takže v něm zbylo 60 litrů vody.

Vypočtěte v litrech objem konvičky.

2.2

Kvádr je možné beze zbytku rozřezat na 200 krychlí, z nichž každá má objem 8 dm³.

Vypočtěte, na kolik krychliček o objemu 1 cm³ lze tento kvádr beze zbytku rozřezat.

3 Vypočtěte a výsledek zapište zlomkem v základním tvaru.

3.1

\frac{5}{9} - \frac{5}{9}: 5 =

3.2

\frac{4-7}{8} \cdot \frac{16}{21} =

3.3

\frac{\frac{3}{5} : \left(\frac{2}{5} + \frac{1}{2}\right)}{\frac{7}{6} + \frac{7}{10} } =

4

4.1 Upravte a rozložte na součin vytknutím:

2\cdot(x^2-x ) +x =

4.2 Umocněte a zjednodušte (výsledný výraz nesmí obsahovat závorky):

(\frac{2}{3}a - 3)^2 =

4.3 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

3n \cdot (2 - n + 2n) + (2n + 1) \cdot (7 - n) =

5 Řešte rovnici:

5.1

0,5x + 2 \cdot (x + 2,5) = 2,5 \cdot (x + 3)

5.2

\frac{y + 10}{15} + \frac{2y}{5} = 1 - \frac{5 - y}{3}

VÝCHOZÍ TEXT K ÚLOZE 6

Pravoúhlý lichoběžník ABCD se základnami AB, CD má pravý úhel při vrcholu C.

Některé rozměry lichoběžníku jsou uvedeny v obrázku.
$Pravoúhlý lichoběžník ABCD se základnami AB, CD má pravý úhel při vrcholu C.$

6 Vypočtěte v cm²

6.1 obsah trojúhelníku ABD,

6.2 obsah lichoběžníku ABCD.

VÝCHOZÍ TEXT A GRAF K ÚLOZE 7

Pouze pro žáky 8. a 9. tříd byly otevřeny tři kroužky – hudební, šachový a robotický.
Každý žák může být jen v jednom z těchto tří kroužků.
Graf znázorňuje počty žáků v jednotlivých kroužcích, jeden údaj a čísla na svislé ose chybí. $Graf s počty žáků v jednotlivých kroužcích.$ V hudebním kroužku je celkem o 6 žáků méně než v šachovém.
Ve všech třech kroužcích dohromady je poměr počtu žáků 8. tříd ku počtu žáků 9. tříd 2 ∶ 3.

7 Určete,

7.1 o kolik procent více je v hudebním kroužku žáků 8. tříd než žáků 9. tříd,

7.2 kolik žáků 9. tříd je v šachovém kroužku,

7.3 jaký je v robotickém kroužku poměr počtu žáků 8. tříd ku počtu žáků 9. tříd.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

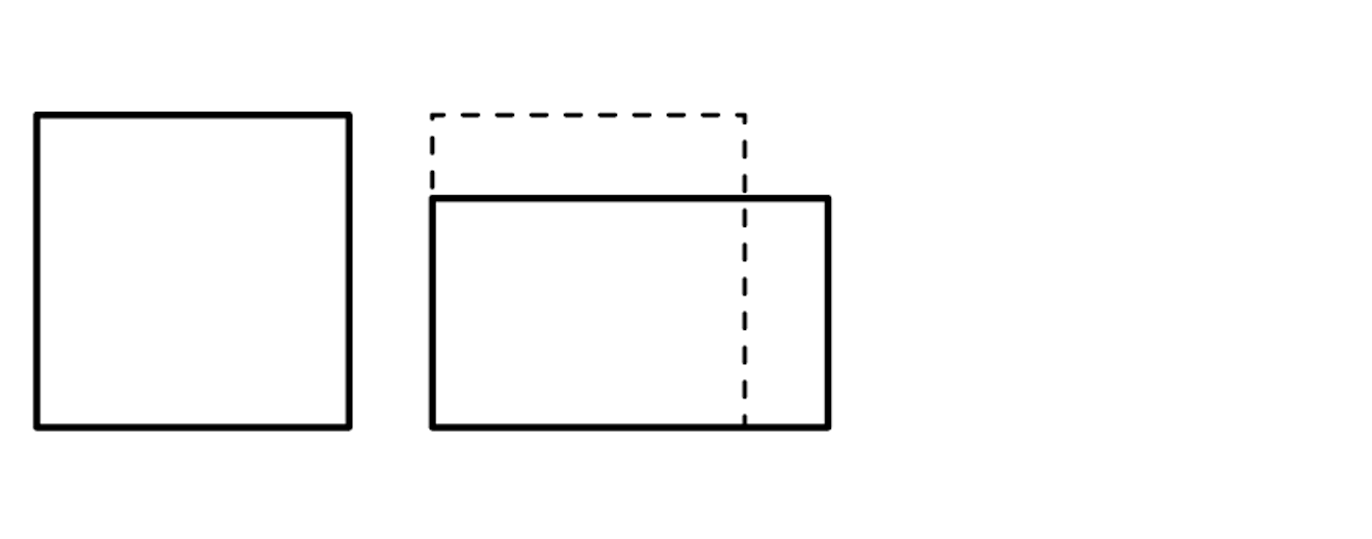
Čtvercový pozemek má stejný obvod jako obdélníkový pozemek. Obdélníkový pozemek má jednu stranu o 25 % kratší než čtvercový pozemek a druhou stranu o 10 m delší než čtvercový pozemek. $Obdélníkový pozemek$

8 Délku strany čtvercového pozemku označíme 𝑎.

8.1 Vyjádřete výrazem s proměnnou 𝑎 délku kratší strany obdélníkového pozemku.

8.2 Vypočtěte v metrech délku 𝑎 strany čtvercového pozemku.

8.3 Vypočtěte, o kolik m^2se liší obsahy obdélníkového a čtvercového pozemku.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

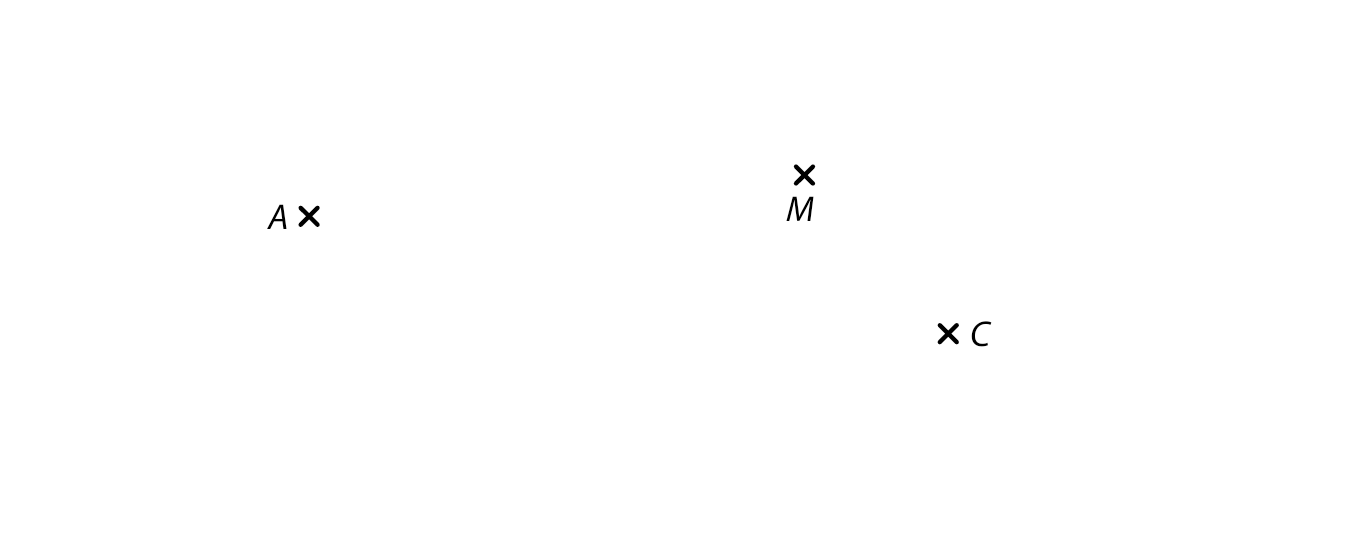
V rovině leží body A, C, M. $Body v rovině$

9

Body A, C jsou vrcholy obdélníku ABCD. Bod M leží na úhlopříčce BD tohoto obdélníku./ Sestrojte vrcholy B, D obdélníku ABCD, označte je písmeny a obdélník narýsujte.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

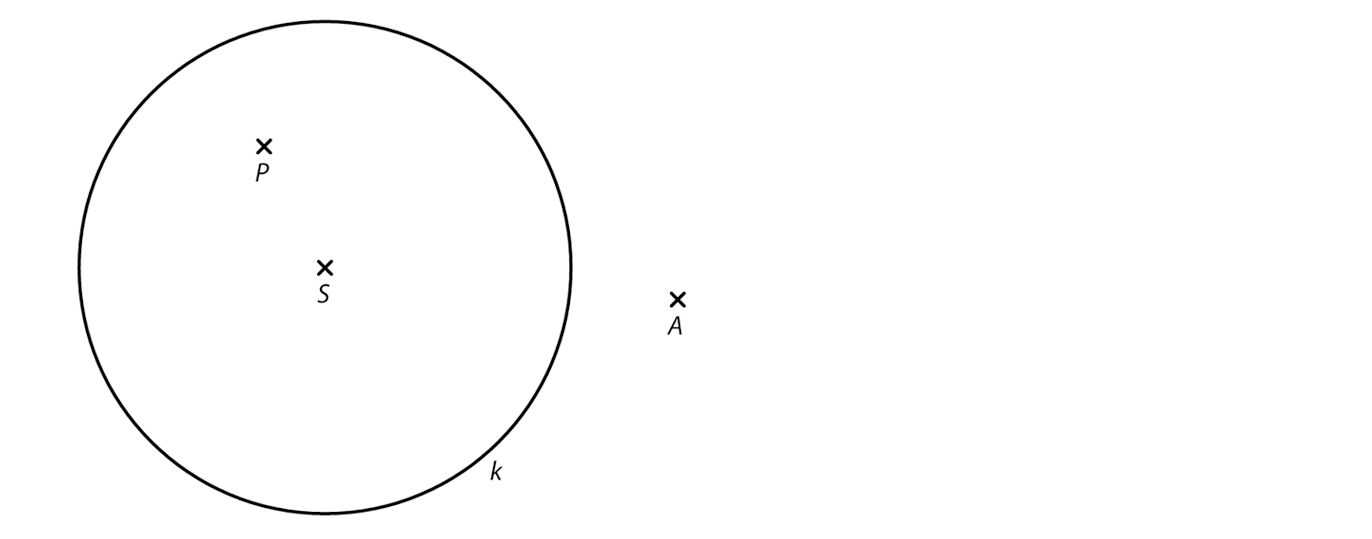
V rovině leží body A, P a kružnice k se středem S. $Kružnice a body v rovině$

10

Bod A je vrchol rovnoramenného trojúhelníku ABC, jehož základna leží na přímce AP.
Vrcholy B, C tohoto trojúhelníku leží na kružnici k.

Sestrojte vrcholy B, C trojúhelníku ABC, označte je písmeny a trojúhelník narýsujte.Najděte všechna řešení

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT K ÚLOZE 11

Každých 3,5 cm na turistické mapě rovinaté oblasti je ve skutečnosti 700 m.
Délka vycházkové trasy je přesně 6 km, což je trojnásobek délky přímé trasy. (Uvažované trasy nemají žádné převýšení.)

11 Rozhodněte o každém z následujících tvrzení (11.1–11.3), zda je pravdivé (A), či nikoli (N).

11.1 Trasa, která na mapě měří 49 mm, je ve skutečnosti delší než 1 km.

11.2 Na mapě je vycházková trasa o 20 cm delší než přímá trasa.

11.3 Měřítko turistické mapy je 1 ∶ 200 000.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12

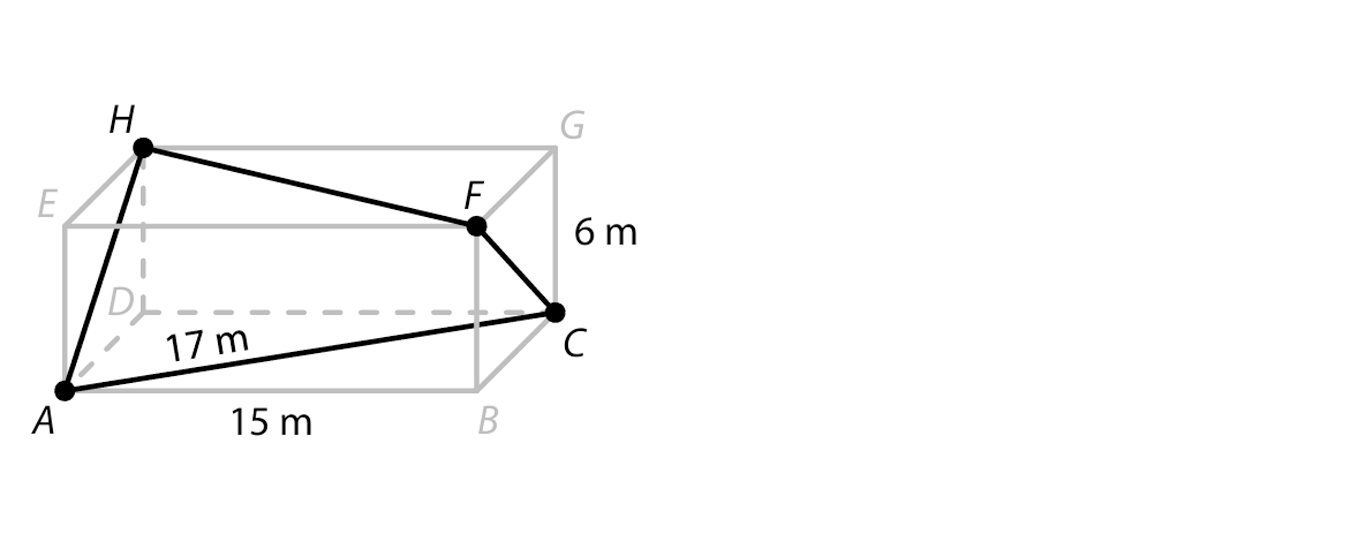
Vnitřní prostor haly má tvar kvádru ABCDEFGH, jehož výška je 6 m a délka 15 m. Uvnitř haly je na podlaze, stropě a dvou stěnách vyznačena uzavřená lomená čára ACFHA. Úhlopříčka vyznačená na podlaze haly měří 17 m a tvoří úsek AC této lomené čáry. $Ilustrace haly$

12 Jaká je délka lomené čáry ACFHA?

46 m

50 m

54 m

68 m

jiná délka

VÝCHOZÍ TEXT K ÚLOZE 13

Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm.

13 Jaký je povrch válce?

Výsledek je zaokrouhlen na desítky cm^2

menší než 930 cm2

940 cm2

1260 cm2

1570 cm2

větší než 1580 cm2

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

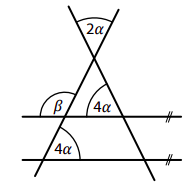
V rovině leží čtyři přímky, z nichž dvě jsou rovnoběžné.

14 Jaká je velikost úhlu 𝛽? Velikosti úhlů neměřte, ale vypočtěte.

100°

108°

116°

120°

jiná velikost

15 Přiřaďte ke každé úloze (15.1–15.3) odpovídající výsledek (A–F).

15.1 V roce 2020 firma vyrobila 250 výrobků.Jak v roce 2021, tak v roce 2022 vyrobila firma vždy o 20 % výrobků více nežv předchozím roce.

Kolik výrobků vyrobila firma v roce 2022?

15.2 Roman i Jana jezdili během dovolené na kole.Roman ujel 400 km, což bylo o čtvrtinu více, než ujela Jana.

Kolik km ujela na kole během dovolené Jana?

15.3 Firma během krize propouštěla zaměstnance,takže jich měla na konci krize o 40 % méně než před krizí.Když firma po odeznění krize přijala 42 nových zaměstnanců,měla jich o 25 % více než na konci krize.

Kolik zaměstnanců měla firma před krizí?

280

300

320

350

360

jiný počet

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16

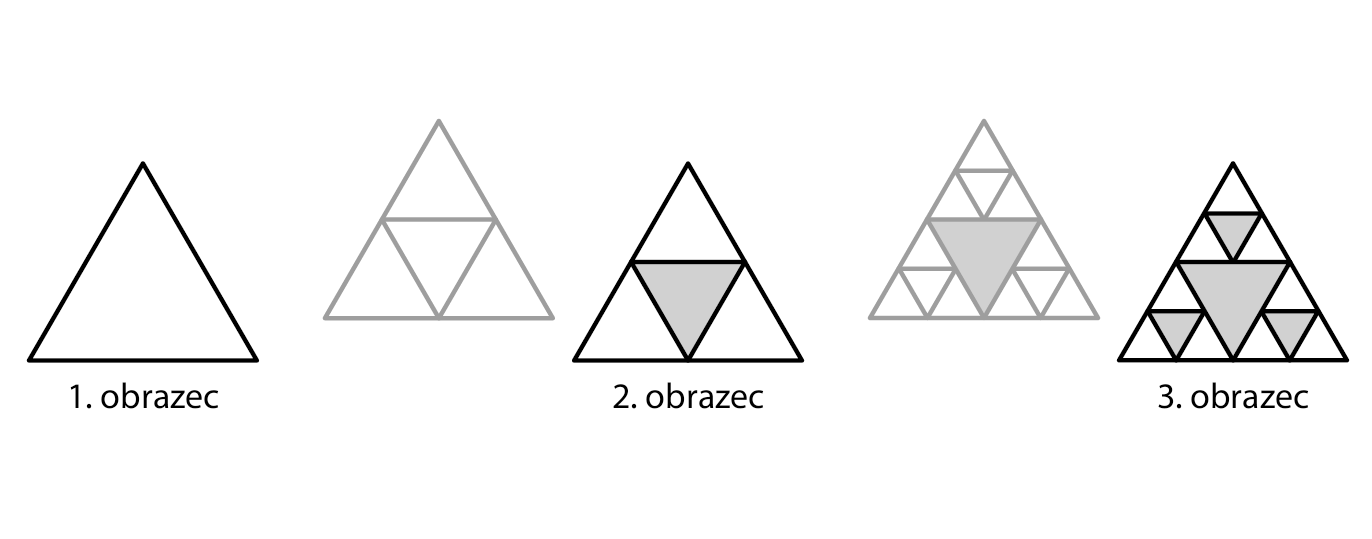
Prvním obrazcem je bílý rovnostranný trojúhelník. Každý další obrazec vznikne z předchozího obrazce dle následujících pravidel:

Nejprve každý bílý trojúhelník v obrazci rozdělíme na 4 shodné rovnostranné trojúhelníky.

Poté v každé takto vzniklé čtveřici bílých trojúhelníků obarvíme vnitřní trojúhelník na šedo. $grafika s trojúhelníky$