1 Pět švadlen, které šíjí oblečení, pracují stejným tempem. Tyto švadleny splní danou zakázku za 24 hodin.

Za jakou dobo splní o polovinu větší zakázku čtyři švadleny?

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 2

Skleněné těžítko má tvar rotačního válce s plolměrem podstavy 10 cm a výškou 12 cm. Vnější část těžítka je z čirého skla, uvnitř je část z modrého skla, která má také tavr rotačního válce, a to s poloměrem podstavy 5 cm a výškou 8 cm.

$alt text$

2 Vypočítejte objem čirého skla v těžítku.

Výsledek zaokrouhlete na desítky cm³. Pro výpočet použijte zaokrouhlenou hodnotu čísla $\pi$ z tabulky na začátku testového sešitu.

3 Vypočítejte a výsledek zapište zlomkem v základním tvaru.

Do záznamového archu uveďte u obou podúloh celý postupu řešení.

3.1

\left(2\div\frac{3}{2}\right)\div\frac{1}{2}+\left(\frac{5}{6}\div\frac{3}{4}\right)\div\frac{2}{3}

3.2

\frac{\frac{13}{10}-1,4}{\frac{2}{15}+\frac{1}{6}}

4 Proveďte úpravu výrazů.

4.1 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

\left(a - \frac{a}{4}\right)^2 =

4.2 Rozložte na součin podle vzorce:

9a^2 - 16 =

4.3 Zjednodušte a výsledek rozložte na součin vytýkáním:

(c-5)\cdot(2-3c)-(c-2c)\cdot3c-c\cdot7=

Do záznamového archu uveďte u podúlohy 4.3 celý postupu řešení.

5 Řešte rovnice.

Do záznamového archu uveďte u obou podúloh celý postupu řešení.
Zkoušku nazapisujte.

5.1

-2\cdot(x+4)-3\cdot(x+1)^2 = x\cdot(2-3x)

5.2

6-\frac{3-2y}{5}\cdot2 = 4y

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 6

Pravoúhlý lichoběžník ABCD se základnami AB a CD má pravý úhel při vrcholu B.
Základna AB má délku 40 cm, základna CD délku 28 cm a úhlopříčka AC délku 41 cm.

$alt text$

6

6.1 Vypočítejte obsah lichoběžníku ABCD.

Výsledek uveďte v cm².

6.2 Vypočítejte délku ramene AD.

Výsledek uveďte v cm.

7 Žáci třídy 8.B se dělí na dvě skupiny podle toho, zda chodí na němčinu nebo angličtinu. V obou skupinách je stejný počet žáků. Ve třídě je 14 chlapců a 5 z nich chodí na angličtinu. Na němčinu chodí 4 dívky.

7.1 Kolik dívek celkem chodí na angličtinu?

7.2 Kolik má třída 8.B celkem žáků?

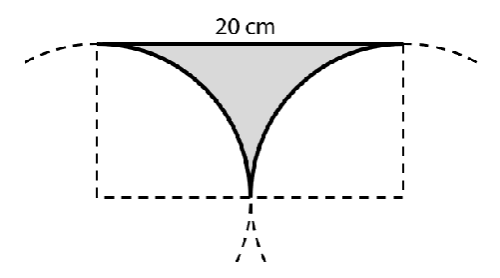
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

Šedý obrazec je ohraničen úsečkou délky 20 cm a dvěma schodnými čtvrtkružnicemi. $alt text$

V podúlohách 8.1 a 8.2 pro výpočet použijte zaokrouhlenou hodnotu čísla $\pi$ z tabulky na začátku testového sešitu.

8.1 Výpočítejte obsah šedého obrazce.

Výsledek uveďte v cm² a zaokrouhlete ho na celé cm².

8.2 Výpočítejte obvod šedého obrazce.

Výsledek uveďte v cm a zaokrouhlete ho na celé cm.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

V rovině leží body C a S. Bod C je vrchol rovnostranného trojúhelníku ABC.
Bod S je středem strany AB.

$alt text$

9 Sestrojte vrcholy A,B rovnostranného trojúhelníku ABC a trojúhleník narýsujte.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

V rovině leží přímka AE a přímka p procházející bodem E. Bod A je vrchol obdelníku ABCD. Vrchol B leží na přímce AE a vrchol C na přímce p. Úhlopříčka BD obdelníku ABCD má stejnou délku jako úsečka AE.

$alt text$

10 Sestrojte vrcholy B,C,D obdelníku ABCD, označte je písmeny a obdelník narýsujte.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11

V rovině leží přímky p, q a r, jejichž průsečíky tvoří vrcholy trojúhelníku ABC.
Jsou dány úhly $\beta = 23\degree$ a $\delta = 107\degree$ .

$alt text$

11 Jaká je velikost rozdílu úhlů $\gamma -\alpha$ ?

Velikost úhlů neměřte, ale vypočítejte (obrázek je ilustrační).

$10\degree$

$11\degree$

$12\degree$

$13\degree$

jiná velikost

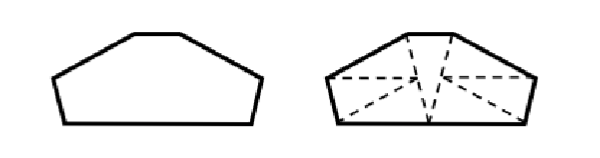
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12

Obrazec je možné rozstříhat na 7 shodných rovnoramenných trojúhelníků.
Obvod jednoho takového trojúhelníku je 30 cm.

$alt text$

12 Jaký je obvod obrazce?

55 cm

60 cm

66 cm

72 cm

90 cm

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

Máme shodné čtverce A a B. Čtverec A je rozdělen na dva shodné obdélníky, čtverec B na pět shodných obdélníků. Obvod jednoho ze dvou obdélníků ve čtverci A je o 6 cm větší než obvod jednoho z pěti obdélníků ve čtverci B.

$alt text$

13 Jaký je obvod jednoho ze čtverců A nebo B?

40 cm

72 cm

80 cm

96 cm

128 cm

14 Vynásobíme-li neznámé číslo dvěma a odečteme-li od výsledku 135, získáme polovinu hodnoty neznámého čísla.

Jaká je hodnota neznámého čísla?

270

170

135

jiný výsledek

15 Půdorys domu má tvar obdélníku. Šířka domu je 10 metrů. V plánu je tato šířka vyznačena úsečkou o délce 10 cm. Délka domu je v plánu zakreslena jako úsečka o délce 2 dm.

Rozhodněte o každém z následujích tvrzení (15.1-15.3), zda je pravdivé (A), či nikoliv (N).

15.1 Měřítko plánu je 1:1 000.

15.2 Skutečná délka domu je 20m.

15.3 Obsah obdélníku na plánu a obsah půdorysu domu jsou v poměru 1:100.

16 Přiřaďte ke každé úloze (16.1-16.3) odpovídající výsledek (A-F).

16.1 Pan Novák si vypůjčil 20 000 Kč na jeden rok. Po roce vrátí věřiteli vypůjčenou částku, a navíc mu zaplatí úrok ve výši 13,5% z vypůjčené částky.

Kolik korun celkem věřiteli vrátí?

16.2 Paní Dlouhá na začátku roku vložila do banky 1 000 000 Kč s roční úrokovou sazbou 2,5%. Výnosy z úroků jsou zdaněny srážkovou daní.

Kolik korun získá paní Dlouhá navíc ke svému vkladu za jeden rok, bude-li jí odečtena daň z úroků 15%?

16.3 Kolo v obchodě stálo 20 000 Kč. Nejdříve bylo zlevněno o 10% z původní ceny, po měsíci bylo zdraženo o 10% z nové ceny.

Jaká byla výsledná cena kola po zlevenění i zdražení?

22 700 Kč

21 350 Kč

21 250 Kč

20 000 Kč

19 800 Kč