1 Vypočtěte:

\sqrt{\left({-5}\right)^{2}}-3^2=

VÝCHOZÍ TEXT K ÚLOZE 2

Třídenní lyžařská permanentka je o 150 % dražší než jednodenní permanentka. Jednodenní permanentka stojí 600 korun. (CZVV)

2 Vypočtěte,

2.1 kolikrát více se zaplatí za třídenní permanentku než za jednodenní permanentku,

2.2 o kolik korun jsou 3 jednodenní permanentky dražší než 1 třídenní permanentka.

Doporučení: Úlohy 3.3, 4.3 a 5 řešte přímo v záznamovém archu.

3 Vypočtěte a výsledek zapište zlomkem v základním tvaru.

3.1

\frac{1}{3}\cdot\frac{1}{2}-\frac{8}{9} =

3.2

\left(2-\frac{5}{6}\right):\frac{5}{3} =

3.3

\frac{\frac{2}{3}+\frac{2}{7}}{\left(\frac{9}{14}+\frac{3}{2}\right)\cdot2} =

V záznamovém archu uveďte pouze v úloze 3.3 celý postup řešení.

4

4.1 Upravte a rozložte na součin vytknutím:

x\cdot(y-3)+3\cdot(x-2y) =

4.2 Určete pomocí vzorce nejjednodušší výraz, kterým je třeba vynásobit výraz $3a-2^2$ , abychom získali výraz $9𝑎^2-16$ .

4.3 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

(3n+2)^2-n\cdot(3n+4)+(2n-n)⋅n =

V záznamovém archu uveďte pouze v úloze 4.3 celý postup řešení.

5 Řešte rovnici:

5.1

2+{0.5}\cdot(x-3)={0.4}\cdot({1.5}x+2)

5.2

3\cdot\frac{2y-1}{6} = \frac{3y+2}{8} + \frac{3}{4}\cdot\frac{y-1}{6}

V záznamovém archu uveďte v obou částech úlohy celý postup řešení (zkoušku nezapisujte).

VÝCHOZÍ TEXT K ÚLOZE 6

V chatě za polárním kruhem jsou připraveny zásoby masa pro 12člennou expedici přesně na 30 dní. Každý člen expedice spotřebuje za den z připravených zásob stejné množství masa.

(CZVV)

6

6.1 Vypočtěte, za kolik dní by 12členná expedice spotřebovala pět šestin připravených zásob masa.

6.2 Vypočtěte, kolikačlenná expedice by všechny připravené zásoby masa spotřebovala za 45 dní.

6.3

Dvě expedice společně spotřebovaly všechny připravené zásoby masa.
První expedice pobývala na chatě 4 dny.
Druhá expedice měla dvakrát více členů než první a pobývala na chatě 8 dní.

Vypočtěte, kolik členů měla první expedice.

VÝCHOZÍ TEXT K ÚLOZE 7

Ondrovi trvá cesta do práce autobusem dvakrát déle než rychlíkem.
Osobním vlakem mu trvá cesta do práce o čtvrtinu déle než autobusem. (CZVV)

7 Dobu Ondrovy cesty do práce autobusem označíme 𝑥.

7.1 Vyjádřete výrazem s proměnnou 𝑥, jak dlouho trvá Ondrovi cesta do práce rychlíkem.

7.2 Vyjádřete výrazem s proměnnou 𝑥, jak dlouho trvá Ondrovi cesta do práce osobním vlakem.

7.3 Cesta do práce trvá Ondrovi rychlíkem o 15 minut méně než osobním vlakem.

Vypočtěte, kolik minut trvá Ondrovi cesta do práce autobusem.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

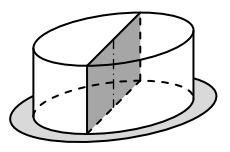
Dort tvaru rotačního válce leží na kruhovém tácu.
(Průměr podstavy dortu je větší než výška dortu, ale menší než průměr tácu.) Dort jsme rozdělili svislým řezem na dvě stejné poloviny.

$dort s podstavou$

(CZVV)

8

8.1 Tác má tvar kruhu o průměru 𝑑 a obsahu π⋅144 cm².

Vypočtěte v cm průměr 𝑑 tácu.

8.2 Plocha řezu dortu má obsah 200 cm² a tvoří ji obdélník, který lze rozdělit na dva čtverce.

Vypočtěte v cm³ objem celého dortu. Výsledek zaokrouhlete na desítky cm³.

Doporučení pro úlohy 9 a 10: Rýsujte přímo do záznamového archu.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

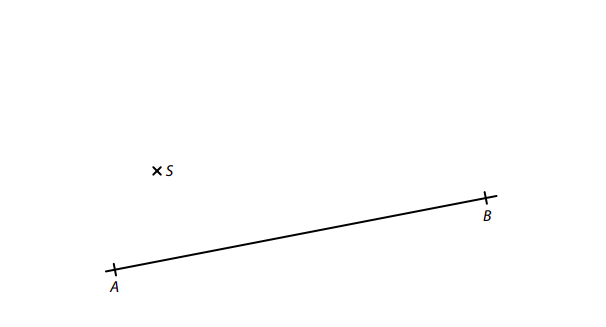
V rovině leží úsečka AB a bod S.

$úsečka AB a bod S v rovině$

(CZVV)

9

Úsečka AB je základna rovnoramenného lichoběžníku ABCD.
Bod S je střed ramene AD tohoto lichoběžníku. Sestrojte vrcholy C, D lichoběžníku ABCD, označte je písmeny a lichoběžník narýsujte. rovnoramenný trojúhelník ABC se základnou AB V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

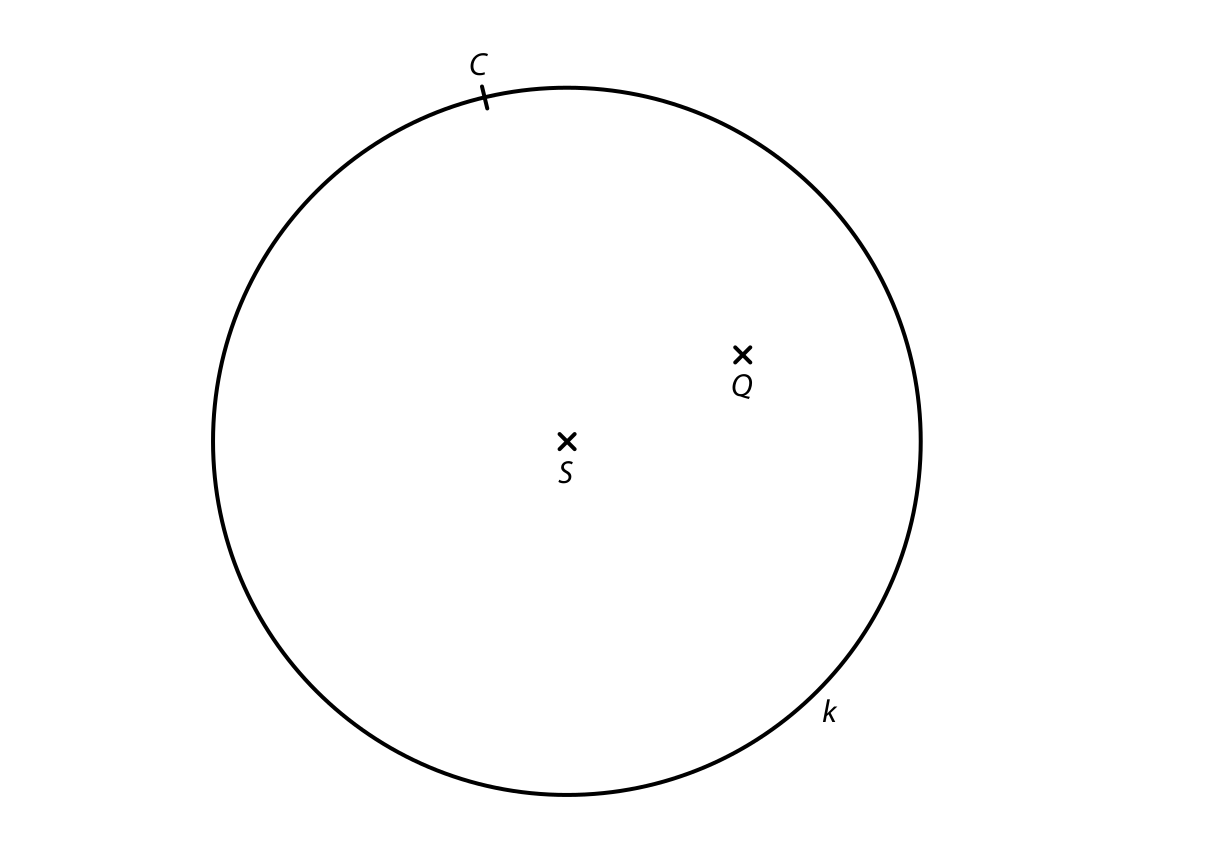
V rovině leží body C, Q a kružnice k se středem S, která prochází bodem C.

$body C, Q a kružnice k se středem S, která prochází bodem C$

(CZVV)

10

Bod C je vrchol trojúhelníku ABC s pravým úhlem při vrcholu C.
Na kružnici k leží také zbývající dva vrcholy A, B tohoto trojúhelníku
a bodem Q prochází jedna jeho strana.

Sestrojte vrcholy A, B trojúhelníku ABC, označte je písmeny a trojúhelník narýsujte.
Najděte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11

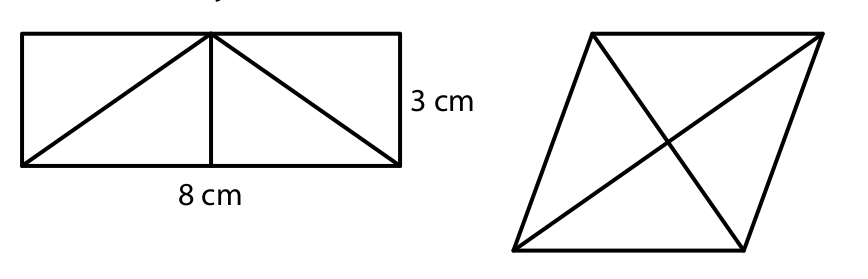
Obdélník se stranami délek 8 cm a 3 cm se skládá ze čtyř shodných trojúhelníků (viz obrázek). Přemístěním trojúhelníků vznikl kosočtverec.

$alt text$

(CZVV)

11 Rozhodněte o každém z následujících tvrzení (11.1–11.3), zda je pravdivé (A), či nikoli (N).

11.1 Obsah kosočtverce je větší než obsah obdélníku.

11.2 Strana kosočtverce měří 5 cm.

11.3 Výška kosočtverce měří 4,8 cm.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12

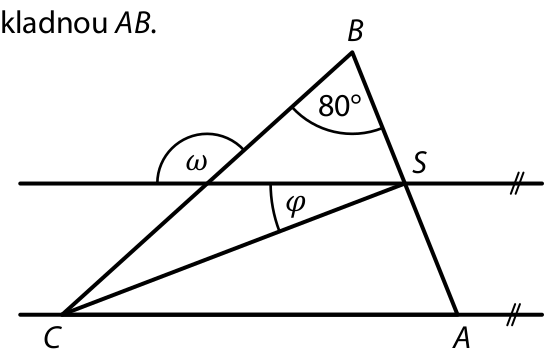
V rovině leží rovnoramenný trojúhelník ABC se základnou AB.
Bod S je střed základny AB a prochází jím
rovnoběžka s přímkou AC.

$alt text$

(CZVV)

12 Jaký je součet $\varphi+\omega$ ?

Velikosti úhlů neměřte, ale vypočtěte.

150°

155°

160°

165°

170°

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

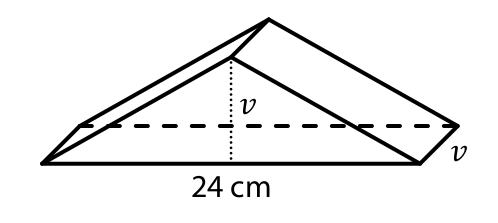
Trojboký hranol je položen na jedné boční stěně.

Podstavu hranolu tvoří rovnoramenný trojúhelník, který má základnu délky 24 cm a obsah 60 cm2.
Velikost 𝑣 výšky na základnu tohoto trojúhelníku je stejná jako délka nejkratší hrany hranolu.

$Trojboký hranol$

(CZVV)

13 Jaký je objem trojbokého hranolu?

150 cm³

200 cm³

300 cm³

370 cm³

jiný objem

VÝCHOZÍ TEXT K ÚLOZE 14

Košíkář prodal během prvních dvou dnů velikonočních trhů všechny upletené pomlázky.
První den prodal pětinu všech upletených pomlázek.
Druhý den prodal o 180 pomlázek více než první den.

(CZVV)

14 Kolik pomlázek prodal košíkář první den velikonočních trhů?

60 pomlázek

45 pomlázek

36 pomlázek

30 pomlázek

jiný počet pomlázek

15 Přiřaďte ke každé úloze (15.1–15.3) odpovídající výsledek (A–F).

15.1 Letos má skautský oddíl 60 členů, což je o 20 členů více než loni.

O kolik procent má letos skautský oddíl více členů než loni?

15.2 Během výletu Jakub utratil tři pětiny kapesného. Tři čtvrtiny z této utracené částky použil k nákupu turistické známky.

Kolik procent z kapesného utratil Jakub za turistickou známku?

15.3 Na třídenním festivalu se první a druhý den prodal stejný počet vstupenek. Třetí den se prodalo o třetinu více vstupenek než druhý den.

Kolik procent všech vstupenek prodaných během festivalu se prodalo třetí den?

méně než 40 %

40 %

45 %

50 %

55 %

více než 55 %

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16

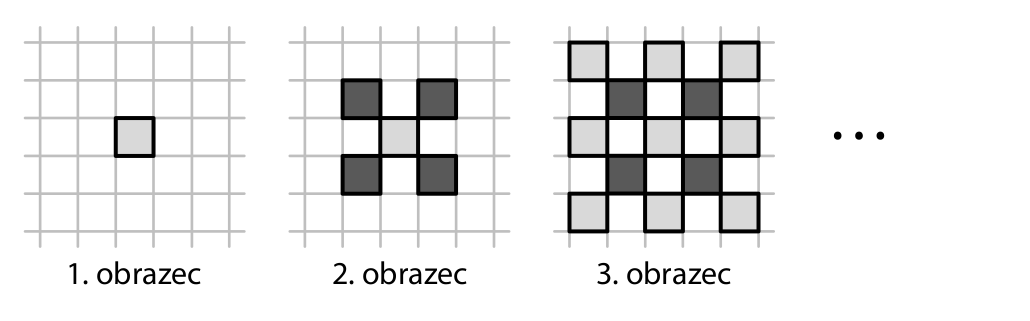
Vybarvováním některých prázdných polí čtvercové sítě postupně vytváříme obrazce.

Prvním obrazcem je jedno světle vybarvené pole čtvercové sítě.

Každý další obrazec vytvoříme z předchozího obrazce tak, že vybarvíme všechna prázdná pole, která mají s předchozím obrazcem společné pouze vrcholy. Tato nově vybarvená pole jsou u sudých obrazců tmavá a u lichých obrazců světlá.

$alt text$

Druhý obrazec jsme vytvořili z prvního obrazce vybarvením 4 dalších polí tmavou barvou. Třetí obrazec má celkem 13 polí (9 světlých a 4 tmavé) a vytvořili jsme jej z druhého obrazce vybarvením 8 dalších polí světlou barvou.

(CZVV)

16 Určete,

16.1 vybarvením kolika dalších polí jsme z 8. obrazce vytvořili 9. obrazec,

16.2 o kolik se liší počet tmavých a světlých polí v 10. obrazci,

16.3 kolik světlých polí může mít obrazec, který má 400 tmavých polí.

Najděte všechna řešení.