1 Josef má délku kroku 75 cm, Naďa má krok dlouhý 60 cm. Josef i Naďa každý ušli 10 000 kroků.

O kolik kilometrů ušel Josef více než Naďa?

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 2

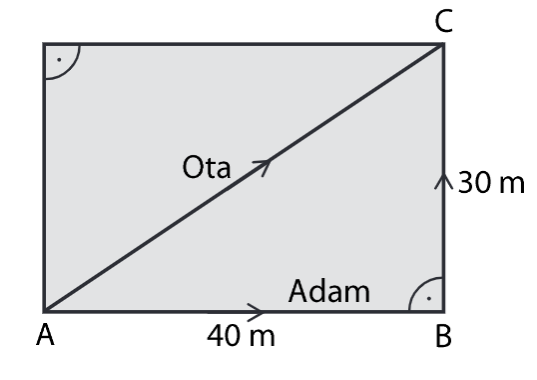
Adam a Ota jsou z místa A do místa C. Každý jde jinou cestou tak, jak je vyznačeno na obrázku. Adam jde z místa A do místa C po rovných silnicích přes místo B. Ota jde zkratkou přímo z A do C.

$alt text$

2 O kolik procent je Adamova cesta delší než cesta, kterou jde Ota?

3 Vypočítejte a výsledek zapište zlomkem v základním tvaru.

Do záznamového archu uveďte u obou podúloh celý postupu řešení.

3.1

\left(\frac{3}{4}+\frac{4}{3}\right)\cdot\left(\frac{2}{3}-\frac{6}{5}\right)

3.2

\frac{\frac{5}{9}-\frac{3}{2}\div\frac{3}{5}}{\frac{2}{3}+\frac{1}{6}-\frac{7}{12}}

4

4.1 Umocněte:

(-3-2x)^2 =

4.2 Upravte a rozložte na součin podle vzorce:

6400 - (x^2-3600) =

4.3 Zjednodušte a výsledek rozložte na součin vytýkáním:

(3x+1)^2-x\cdot7x-(2x-5)\cdot(x+4)=

Do záznamového archu uveďte u podúlohy 4.3 celý postupu řešení.

5 Řešte rovnice.

Do záznamového archu uveďte u obou podúloh celý postupu řešení.
Zkoušku nazapisujte.

5.1

1,6\div2-\frac{x}{2}= 3\cdot0,7x+3,4

5.2

\frac{5-2y}{3}+\frac{y}{9} = \frac{3-y}{6}

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 6

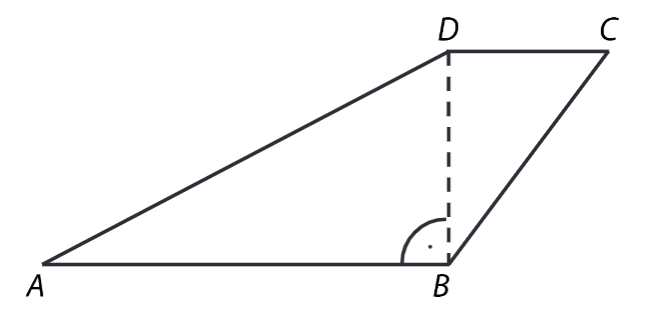
Čtyřúhelník ABCD je takový lichoběžník se základnami AB a CD, že úsečka BD je jeho výška. Pro délky stran platí |AD| = 17cm, |BD| = 18cm, obsah trojúhelníku BCD je S = 24 cm².

$alt text$

6

6.1 Vypočítejte obsah lichoběžníku ABCD.

Výsledek uveďte v cm².

6.2 Vypočítejte obvod lichoběžníku ABCD.

Výsledek uveďte v cm.

7 Petr sbírá modely aut. Druhý rok nasbíral o polovinu počtu modelů aut více, než které nasbíral první rok. Třetí rok nasbíral 72 modelů. Počet modelů, které Petr nasbíral v prvním roce, označte x.

7.1 V závislosti na veličině x vyjádřete, kolik modelů nasbíral Petr během druhého roku.

7.2 Vypočítejte, kolik modelů nasbíral Petr během prvního roku, pokud za tři roky nasbíral 217 modelů.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

Obrazce jsou tvořeny z velkých bílých a malých tmavých kruhů podle určitého pravidla. První obrazec tvoří jeden velký bílý kruh. Druný obrazec tvoří čtyři bílé kruhy, jejichž středy tvoří vrcholy čtverce, a jeden tmavý kruh uprostřed. Každé dva sousední kruhy mají společný právě jeden bod. Třetí obrazec je sestaven za dodržení pravidla vytváření obrazců tak, že je tvoří devět bílých kruhů a čtyři kruhy tmavé. Daným způsobem sestavujeme další obrazce.

$alt text$

8

8.1 Kolik velkých bílých kruhů obsahuje osmý obrazec?

8.2 Kolikátý obrazec obsahuje 361 malých tmavých kruhů?

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

V rovnině jsou dány body A,B a O. Body A,B jsou vrcholy kosočtverce ABCD.
Vrchol C kosočtverce leží na přímce OA.

$alt text$

9 Sestrojte kosočtverec ABCD.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

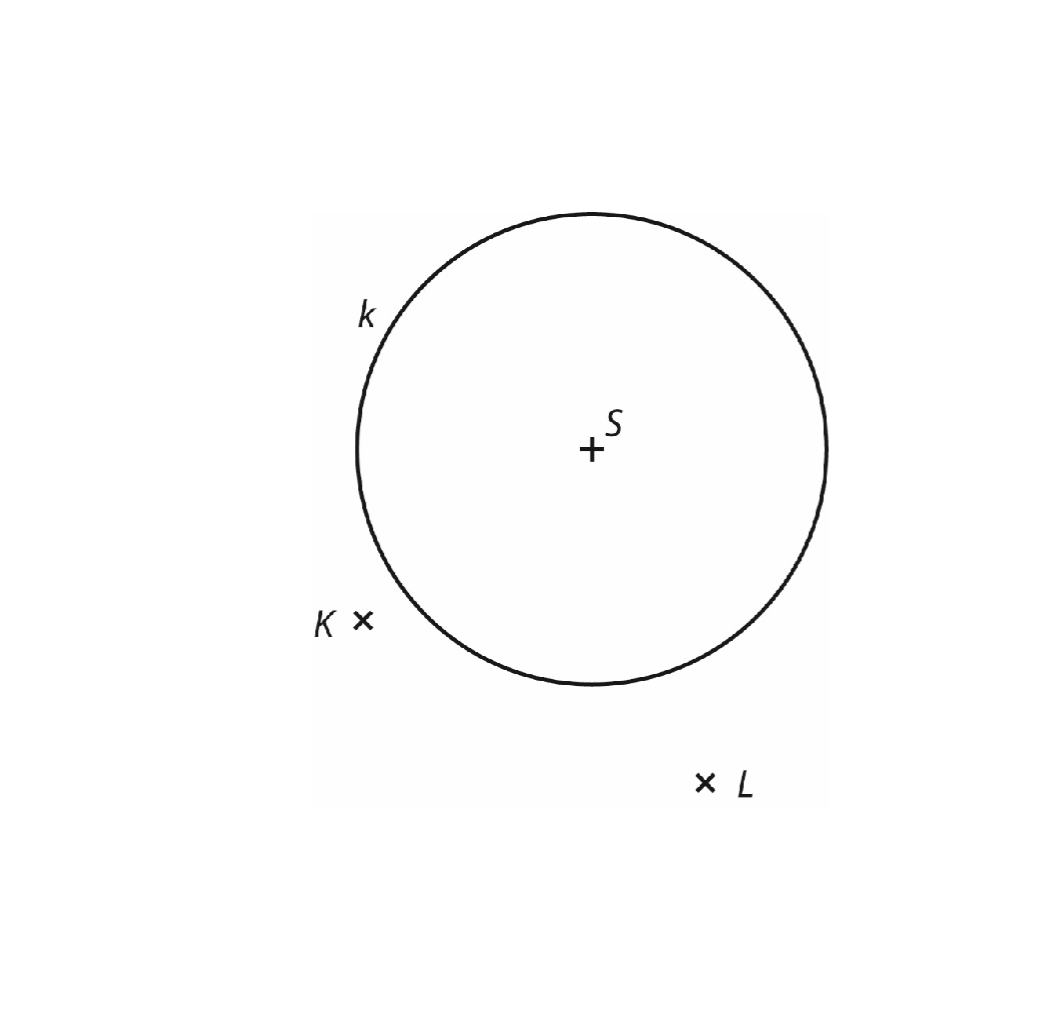
V rovině je dána kružnice k se středem S a body K,L.
Body K,L jsou vrcholy rovnoramenného trojúhelníku KLM se základnou LM.

$alt text$

10 Sestrojte rovnoramenný trojúhelník KLM, leží-li bod M na kružnici k.

Nalezněte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).

11 Hračka stála 250 korun. Nejdříve byla zdražena o 40 % oproti původní ceně, po měsíci pak byla zlevněna o 40 % z nové ceny.

Kolik stála hračka po této dvojí úpravě cen?

220 Kč

210 Kč

230 Kč

250 Kč

280 Kč

12 Pekař na trhu prodával malé a velké koláčky. Velký koláček byl o polovinu dražší než malý koláček a stál 30 Kč. Velké koláčky prodal pekař všechny a utržil za ně 3 000 Kč. Desitinu malých koláčků neprodal a za prodané malé koláčky utržil 3 600 Kč.

Kolik pekař původně přivezl na trhu malých koláčků?

100

180

200

240

jiný počet

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

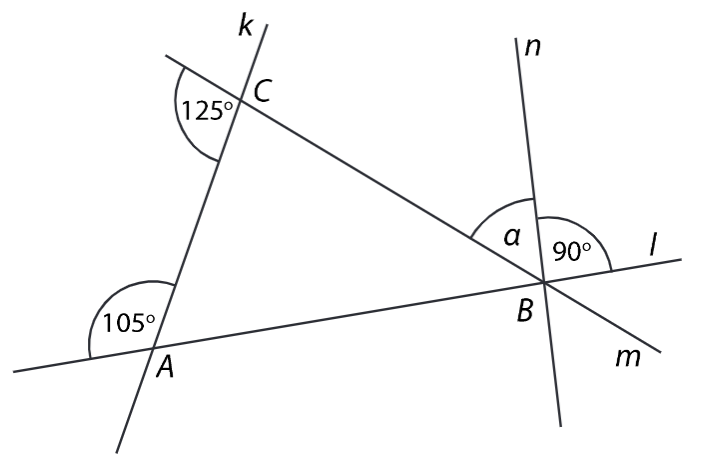
V rovině leží přímky k,l,m a n. Průsečíky přímek k,l a m tvoří vrcholy trojúhelníku ABC.
Bodem B prochází také přímka n.

$alt text$

13 Jaká je velikost úhlů $\alpha$ ?

Velikost úhlů neměřte, ale vypočítejte (obrázek je ilustrační).

55°

50°

45°

40°

35°

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

Ve čtvercové síti je zakreslen šedý obrazec - půlkruh s průměrem AB. Body A a B leží v mřížových bodech. Délka strany čtverce ve čtvercové síti je 2 cm.

$alt text$

14 Jaký je obsah šedé části?

Pro výpočet použijte zaokrouhlenou hodnotu čísla $\pi$ z tabulky na začátku testového sešitu.

20,28 cm²

22,56 cm²

24,56 cm²

25,12 cm²

30,24 cm²

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 15

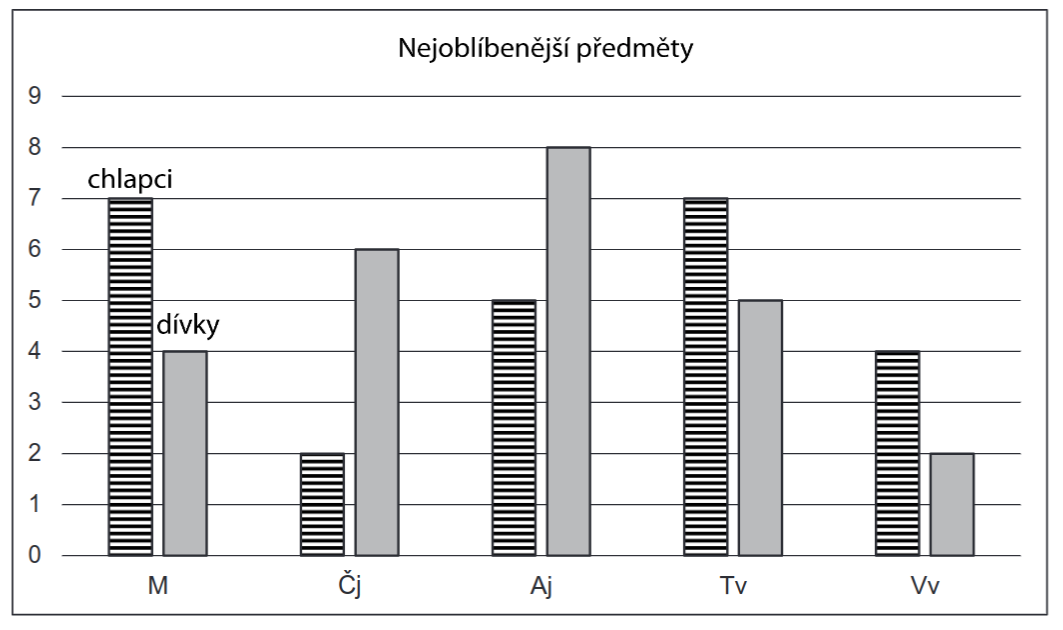
Žáci 9. ročníku mezi sebou provedli statistický průzkum. Každý žák volil svou nejoblíbenější předmět, přičemž každý si zvolil právě jeden. Výsledky jsou zaznamenány v grafu.

$alt text$

15 Rozhodněte o každém z následujích tvrzení (15.1-15.3), zda je pravdivé (A), či nikoliv (N).

15.1 V 9.ročníku je stejný počet dívek jako chlapců.

15.2 Český jazyk volilo více než 16 % všech žáků 9. ročníku.

15.3 Počet chlapců, kteří volili matematiku, je o 75 % větší než počet děvčat, která volila také matematiku.

16 Přiřaďte ke každé úloze (16.1-16.3) odpovídající výsledek (A-F).

16.1 Lyžařský pobyt stál celkem 7 000 Kč. Cena zarhnovala dopravu, ubytování a lístek na vlek. Doprava tvořila desitinu celkové ceny, 60 % ceny stálo ubytování.

Kolik procent ceny pobytu tvořila cena lístku na vlek?

16.2 Cena učebnice matematiky se snížila na částku 1 500 Kč z původních 2 000 Kč.

Kolik procent činila sleva?

16.3 Petr přivezl nemocnému kamarádovi dárek ze zahraničních zájezdu za 40 EUR. Celkem měl vyměněno 200 EUR.

Kolik procent z vyměněných EUR tvořila cena dárku?

15 %

20 %

25 %

30 %

40 %

jiný výsledek