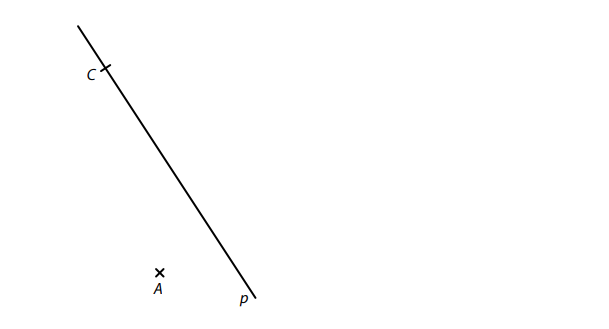1 Vypočtěte, kolikrát je součet čísel 0,2 a 0,5 větší než jejich součin.

2 Vypočtěte:

2.1

4+6÷2−5⋅(−3+5)=4+6\div2-5\cdot(-3+5)=

2.2

1,32−1,22=\sqrt{1,3^2-1,2^2}=

3 Vypočtěte a výsledek zapište zlomkem v základním tvaru.

3.1

3⋅27−27=3\cdot\frac{2}{7}-\frac{2}{7}=

3.2

1−145÷2=1-\frac{14}{5}\div2=

3.3

34+4357⋅143=\frac{\frac{3}{4}+\frac{4}{3}}{\frac{5}{7}\cdot\frac{14}{3}}=

4

4.1 Rozložte na součin podle vzorce:

4a2−9=4a^2-9=

4.2 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

(2x−1)⋅12−x=(2x-1)\cdot\frac{1}{2}-x=

4.3 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

(4n−3)2−4n⋅(4n−3)=(4n-3)^2-4n\cdot(4n-3)=

5 Řešte rovnici:

5.1

0,3⋅(2x+1)=0,2x−0,70,3\cdot(2x+1)=0,2x-0,7

5.2

y+5y6=2y−14+y+12y+\frac{5y}{6}=\frac{2y-1}{4}+\frac{y+1}{2}

VÝCHOZÍ TEXT K ÚLOZE 6

Vítek, Rudolf a Ondra jeli společně autem k moři. Každý z nich odřídil část trasy.

Vítek odřídil třetinu celé trasy, Rudolf odřídil o 60 km méně než Vítek a Ondra odřídil zbývající dvě pětiny celé trasy.

(CZVV)

6 Celá trasa měřila 𝑥 km.

6.1 Vyjádřete výrazem s proměnnou 𝑥, kolik km trasy odřídil Rudolf.

6.2 Vypočtěte, kolik km měřila celá trasa.

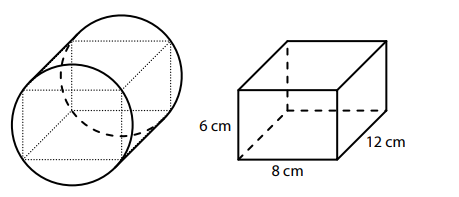
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7

Rotační válec má výšku 12 cm.
Odstraněním čtyř částí vytvoříme z tohoto válce kvádr s rozměry 8 cm, 6 cm a 12 cm.
Všechny hrany kvádru leží na povrchu válce.

alt text

(CZVV)

7 Vypočtěte

7.1 v cm poloměr podstavy válce,

7.2 v cm3 objem válce.

Výsledek zaokrouhlete na desítky cm3.

VÝCHOZÍ TEXT A TABULKA K ÚLOZE 8

V obchodě s oříšky prodávají různé směsi. Jejich cena závisí pouze na hmotnosti a ceně použitých surovin. Tabulka udává ceny za 1 kg jednotlivých surovin.

Surovina Cena za 1 kg
Arašídy 80 korun
Kešu 280 korun
Mandle 200 korun

(Např. 200gramové balení směsi obsahující 50 gramů kešu a 150 gramů mandlí stojí 44 korun, tedy 1 kg této směsi stojí 220 korun.)

(CZVV)

8

8.1 Dvoukilogramové balení směsi arašídů a mandlí obsahuje 800 gramů arašídů a 1 200 gramů mandlí.

Vypočtěte, kolik korun stojí jeden kilogram této směsi.

8.2 Jiná směs obsahuje pouze arašídy a kešu, přičemž 1 kg této směsi stojí 200 korun. Velké balení této směsi obsahuje 500 gramů arašídů.

Vypočtěte, kolik gramů kešu obsahuje velké balení této směsi.

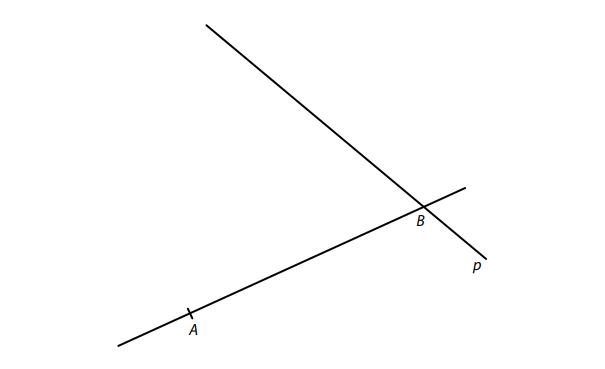
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

V rovině leží přímka AB a přímka p procházející bodem B.

alt text

(CZVV)

9

Úsečka AB je strana pravoúhlého lichoběžníku ABCD.
Vrchol C tohoto lichoběžníku leží na přímce p,
úhlopříčka AC má stejnou délku jako strana AB lichoběžníku ABCD. Sestrojte vrcholy C, D lichoběžníku ABCD, označte je písmeny a lichoběžník narýsujte.

Najděte všechna řešení.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

V rovině leží body A, C a přímka p procházející bodem C.

alt text

(CZVV)

10

Úsečka AC je základna rovnoramenného trojúhelníku ABC.
Na přímce p leží jedna ze tří výšek tohoto trojúhelníku.

10.1 Sestrojte osu souměrnosti trojúhelníku ABC a označte ji písmenem o.

10.2 Sestrojte vrchol B trojúhelníku ABC, označte ho písmenem a trojúhelník narýsujte.

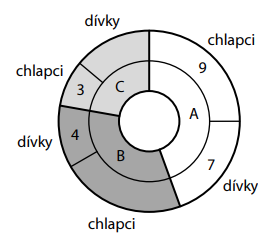
VÝCHOZÍ TEXT A GRAF K ÚLOZE 11

Na táboře je každé dítě zařazeno do jednoho ze tří oddílů A, B a C. V oddíle A je dvakrát více dětí než v oddíle C. Poměr počtu dětí v oddíle A ku počtu dětí v oddíle B je 4∶3. Graf udává počty chlapců a dívek v jednotlivých oddílech, dva údaje však chybí.

alt text

(CZVV)

11 Rozhodněte o každém z následujících tvrzení (11.1–11.3), zda je pravdivé (A), či nikoli (N).

11.1 V oddíle C je 5 dívek.

11.2 V oddíle B je chlapců o polovinu více než dívek.

11.3 Na táboře je dívek o pětinu méně než chlapců.

VÝCHOZÍ TEXT K ÚLOZE 12

Ve vlakové soupravě jsou pouze stejně dlouhé vagony a jedna lokomotiva.

Lokomotiva je o čtvrtinu kratší než jeden vagon a její délka tvoří jednu sedmnáctinu délky celé vlakové soupravy.

(CZVV)

12 Kolik vagonů je celkem ve vlakové soupravě?

A)

10 vagonů

B)

11 vagonů

C)

12 vagonů

D)

13 vagonů

E)

jiný počet vagonů

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

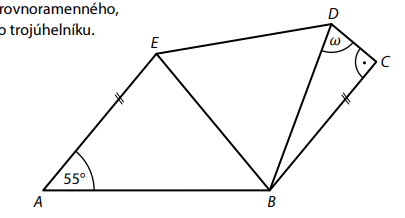
Pětiúhelník ABCDE se skládá z rovnoramenného, rovnostranného a pravoúhlého trojúhelníku.
Základnou rovnoramenného Trojúhelníku je strana AB.
Strany BC a AE pětiúhelníku jsou rovnoběžné.

alt text

(CZVV)

13 Jaká je velikost úhlu 𝜔?

Velikosti úhlů neměřte, ale vypočtěte.

A)

65°

B)

70°

C)

75°

D)

80°

E)

jiná velikost

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

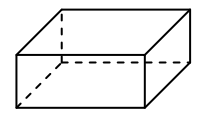
Povrch pravidelného čtyřbokého hranolu je 144 cm2.
Obsah pláště tohoto hranolu je dvakrát větší než obsah jedné jeho čtvercové podstavy.
(Plášť tohoto hranolu tvoří čtyři shodné boční stěny.)

alt text

(CZVV)

14 Jaký je objem hranolu?

A)

72 cm3

B)

108 cm3

C)

144 cm3

D)

216 cm3

E)

jiný objem

15 Přiřaďte ke každé úloze (15.1–15.3) odpovídající výsledek (A–F).

15.1 Encyklopedie má o 25 % více stran než atlas, který má 200 stran.

Kolik stran má encyklopedie?

15.2 Róza čte knihu, která má 500 stran. Počet stran, které Róza již přečetla, je o 50 % větší než počet stran, které dosud nepřečetla.

Kolik stran knihy Róza dosud nepřečetla?

15.3

V knihovně jsou některé knihy psané německy, jiné anglicky a ostatní česky.

Německy psaných je 30 knih, což je 10 % všech knih v knihovně. Anglicky psané knihy tvoří pětinu všech knih v knihovně.

Kolik je v knihovně česky psaných knih?

A)

méně než 210

B)

210

C)

220

D)

240

E)

250

F)

jiný počet

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16

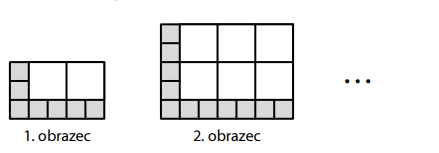
Každý obrazec tvaru obdélníku je složen z malých šedých čtverečků a větších bílých čtverečků. Všechny šedé čtverečky jsou stejné a jsou poskládány do spodní řady a do levého sloupce. Zbytek obrazce tvoří bílé čtverečky. Každý bílý čtvereček má dvakrát delší stranu než šedý.

První obrazec má ve spodní řadě 5 šedých čtverečků a v levém sloupci 3 šedé čtverečky. Skládá se celkem z 9 čtverečků (bílých i šedých dohromady).

Každý další obrazec má oproti předchozímu vždy o 2 šedé čtverečky více jak ve spodní řadě, tak i v levém sloupci.

alt text

(CZVV)

16

16.1 Obrazec má ve spodní řadě 41 šedých čtverečků.

Určete počet bílých čtverečků v obrazci.

16.2 V obrazci je 90 bílých čtverečků.

Určete počet šedých čtverečků v obrazci.

16.3 Počet všech čtverečků (bílých i šedých dohromady) v posledním a v předposledním obrazci se liší o 106.

Určete počet šedých čtverečků v posledním obrazci.