1 Města Jihlava a Třebíč mají dohromady 86 200 obyvatel. Jihlava má o 16 000 obyvatel více.
Kolik obyvatel má Třebíč?
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 2
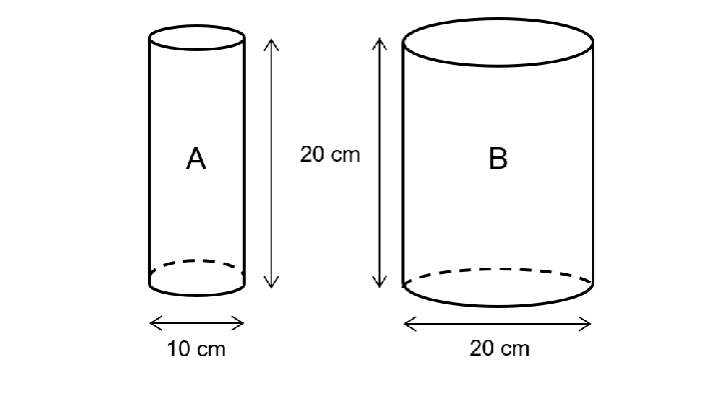
Dvě válcové nádoby A a B mají stejnou výšku v = 20 cm. Nádoba A má průměr podstavy d1 = 10 cm, nádoba B má průměr podstavy d2 = 20 cm. Nádoba A je naplněna až po okraj vodou, nádoba B je prázdná.
2 Do jaké výšky bude sahat voda v nádobě B, pokud všechnu vodu z nádoby A přelijeme do nádoby B?
Pro výpočet použijte zaokrouhlenou hodnotu čísla π z tabulky na začátku testového sešitu.
3 Vypočítejte a výsledek zapište zlomkem v základním tvaru.
Do záznamového archu uveďte u obou podúloh celý postup řešení.
3.1
3.2
4 Proveďte úpravu výrazů.
4.1 Umocněte a zjednodušte.
Výsledek zapište zlomkem v základním tvaru.
4.2 Upravte a výsledný výraz rozložte na součin pomocí vzorců:
4.3 Zjednodušte (výsledný výraz nesmí obsahovat závorky):
Do záznamového archu uveďte u podúlohy 4.3 celý postup řešení.
5 Řešte rovnice.
Do záznamového archu uveďte u obou podúloh celý postup řešení. Zkoušku nezapisujte.
5.1
5.2
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 6
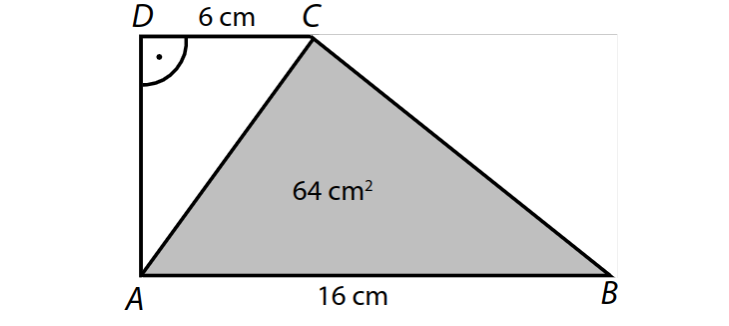
Pravoúhlý lichoběžník ABCD se základnami AB a CD a s pravým úhlem při vrcholu D je úhlopříčkou AC rozdělen na dva trojúhelníky ABC a ACD.
Pro délky stran platí: |AB| = 16 cm, |CD| = 6 cm. Obsah trojúhelníku ABC je 64 cm2.
6
6.1 Vypočítejte výšku lichoběžníku ABCD.
Výsledek uveďte v cm.
6.2 Vypočítejte obsah lichoběžníku ABCD.
Výsledek uveďte v cm2.
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7
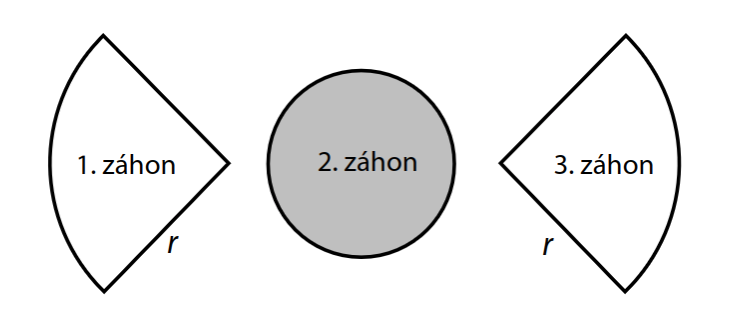
V parku jsou 3 okrasné záhony. První a třetí záhon o stejné velikosti mají tvar čtvrtkruhu, druhý záhon má tvar kruhu. Každý ze tří záhonů má obsah 314 dm2.
7
V podúlohách 7.1 a 7.2 pro výpočet použijte zaokrouhlenou hodnotu čísla π z tabulky na začátku testového sešitu.
7.1 Vypočítejte obvod druhého (kruhového) záhonu.
Výsledek uveďte v celých metrech.
7.2 Vypočítejte poloměr r jednoho z čtvrtkruhových záhonů.
Výsledek uveďte v celých metrech.
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8
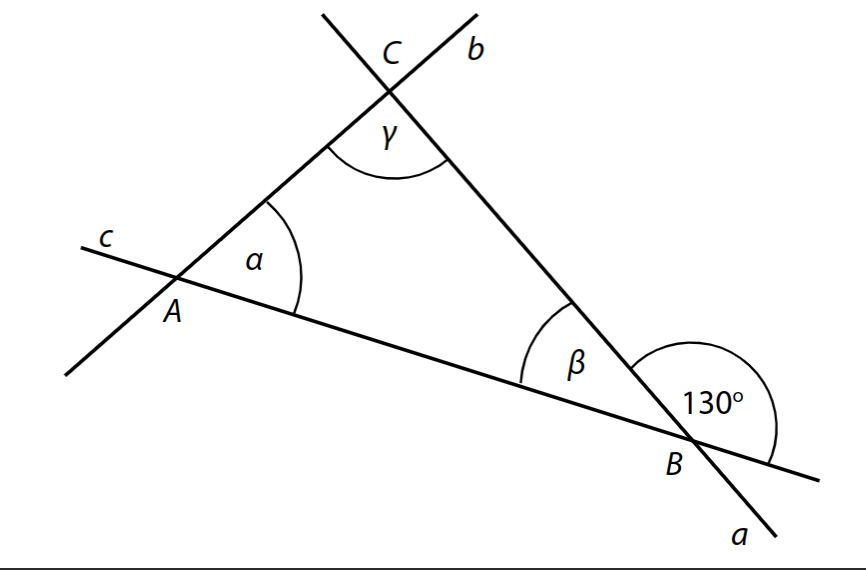
Trojúhelník ABC je vymezen třemi různoběžkami a, b, c. Přímky a a c svírají úhel 130° a velikosti úhlů α a γ jsou v poměru 2:3.
8
8.1 Vypočítejte velikost vnitřního úhlu γ při vrcholu C.
8.2 Vypočítejte rozdíl α – β vnitřních úhlů α a β.
Velikosti úhlů neměřte, ale vypočítejte (obrázek je ilustrační).
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9
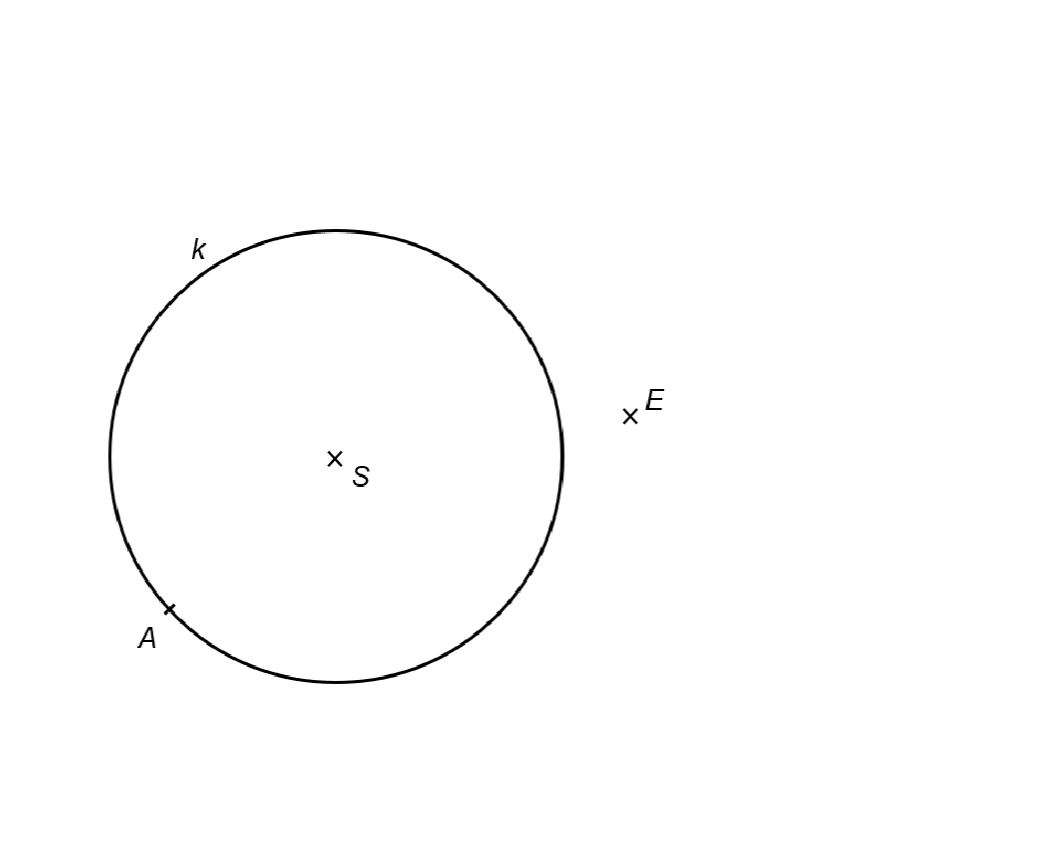
SV rovině leží bod E a kružnice k se středem S, která prochází bodem A. Bod A je vrchol pravoúhlého lichoběžníku ABCD se základnami AB a CD a pravým úhlem při vrcholu A. Vrcholy C a D tohoto lichoběžníku leží na kružnici k, bod E je střed ramene BC.
9 Sestrojte zbývající vrcholy B, C a D lichoběžníku ABCD, označte je písmeny a lichoběžník narýsujte.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10
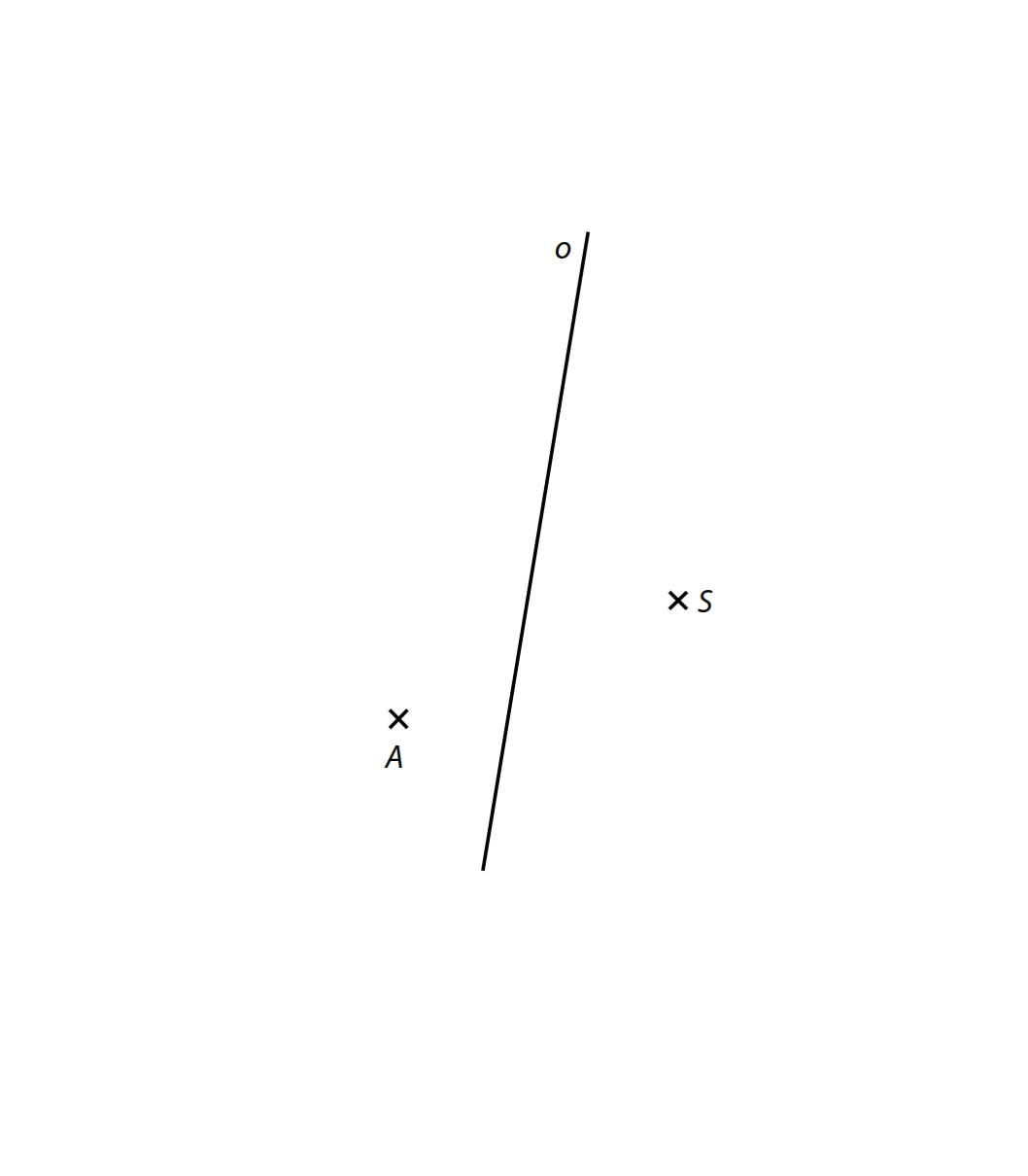
V rovině je dána přímka o a body A a S, které neleží na přímce o. Bod A je vrchol rovnoramenného lichoběžníku ABCD, bod S je střed strany BC. Přímka o je osa souměrnosti lichoběžníku.
10 Sestrojte lichoběžník ABCD.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11
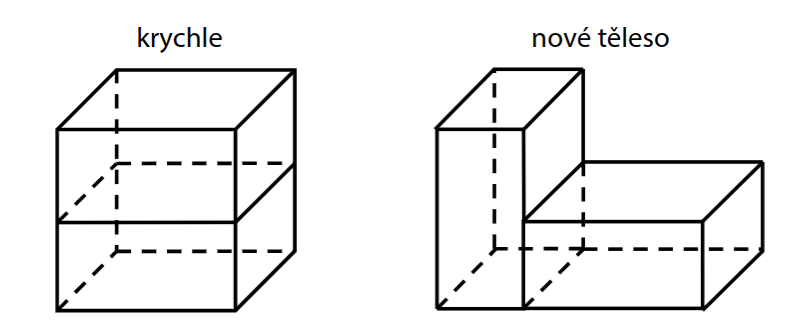
Krychle má délku hrany 3 dm. Krychli rozdělíme vodorovným řezem na dva shodné hranoly a vytvoříme nové těleso.
11 O kolik dm2 se zvětší povrch nového tělesa?
o 4,5 dm2
o 9 dm2
o 18 dm2
oba povrchy jsou stejné
jiný výsledek
12 Dva sourozenci Eva a Michal šetří společně na dárek pro rodiče. Eva našetřila 40 % potřebné částky, Michal o 24 korun více než Eva. Sourozencům zbývá našetřit 72 korun.
Kolik korun stojí dárek?
96 Kč
120 Kč
480 Kč
1 920 Kč
jiný výsledek
13 V divadle bylo těsně před začátkem představení v sále obsazeno 70 % sedadel. Po začátku představení přišlo se zpožděním ještě 11 lidí a obsazenost sálu se tím zvýšila na 75 %.
**Jaká je kapacita sálu? **
méně než 200
200
210
220
více než 220
14 Tři kamarádi Petr, Cyril a Honza čtou komiksy. Petr přečetl o 3 komiksy více než Cyril, Honza přečetl o osminu komiksů více než Cyril. Petr a Honza přečetli stejný počet komiksů.
Kolik komiksů přečetl Petr?
22
24
25
26
27
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 15
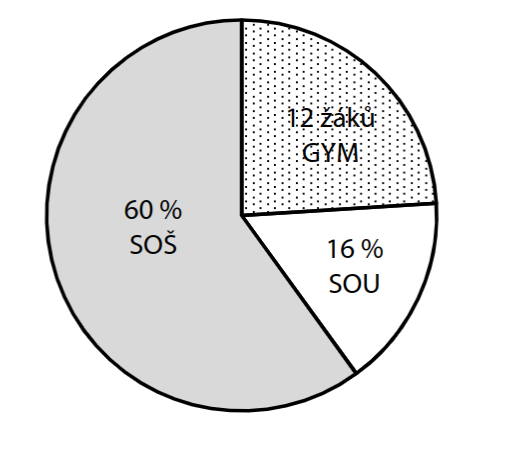
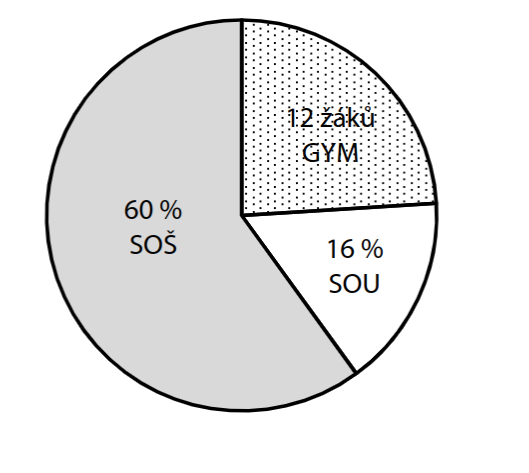
Všichni žáci 9. A a 9. B odpověděli v průzkumu, jakou střední školu chtějí studovat. Žáci chtějí na gymnázia (GYM), střední odborné školy (SOŠ) nebo střední odborná učiliště (SOU). Ti, kteří chtějí na střední odbornou školu, uvedli také obor zaměření – humanitní, technický či umělecký. Výsledky průzkumu jsou zaznamenány v grafech. Na gymnázia chce jít studovat 12 žáků. Nejmenší zájem je o odborná učiliště, kam chce jít 16 % žáků. Největší zájem je o střední odborné školy, na kterých chtějí studovat všichni, kteří nechtějí jít na gymnázia ani na odborná učiliště. Na uměleckou střední školu chtějí 3 žáci, 15 žáků na technicky zaměřenou střední školu, ostatní, kteří chtějí na střední odborné školy, by si vybrali humanitní obor.
Zájem o gymnázia, SOŠ a SOU
SOŠ podle zaměření
15 Rozhodněte o každém z následujících tvrzení (15.1–15.3), zda je pravdivé (A), či nikoli (N).
15.1 Na uměleckou střední školu chce jít 6 % všech žáků.
15.2 V 9. A a 9. B je celkem více než 50 žáků.
15.3 Na gymnázia a na humanitní střední školy se chce hlásit stejný počet žáků.
16 Deset zedníků dokončí stavbu budovy za 20 dní. Všichni zedníci jsou stejně výkonní a pracují rovnoměrným tempem.
Přiřaďte ke každé úloze (16.1–16.3) odpovídající výsledek (A–F).
16.1 Za kolik dní dokončí stavbu budovy 4 zedníci?
16.2 Kolik zedníků dokončí stavbu budovy za 5 dní?
16.3 Kolik dní bude trvat dokončení stavby budovy, jestliže na první polovině stavby pracuje 8 zedníků a současně na druhé polovině stavby pracuje 10 zedníků?
10
12,5
22,5
40
50
52,5