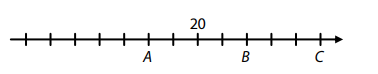1 Hmotnosti dvou závaží jsou v poměru 3∶5 a liší se o 600 g.

Vypočtěte v gramech hmotnost lehčího závaží.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 2

Na číselné ose je vyznačeno 13 bodů, které oddělují 12 stejných dílků.
V jednom z těchto bodů je číslo 20 a body A, B, C představují tři kladná čísla.

Číslo v bodě C je součtem čísla v bodě A a čísla v bodě B.

alt text

(CZVV)

2 Určete číslo v bodě

2.1 C,

2.2 B.

Doporučení: Úlohy 3.3, 4.3 a 5 řešte přímo v záznamovém archu.

3 Vypočtěte a výsledek zapište zlomkem v základním tvaru.

3.1

23−189=\frac{\frac{2}{3}-1}{\frac{8}{9}}=

3.2

2⋅16−38⋅4=2\cdot\frac{1}{6}-\frac{3}{8}\cdot4=

3.3

67−91487+67÷32=\frac{\frac{6}{7}-\frac{9}{14}}{\frac{8}{7}+\frac{6}{7}\div\frac{3}{2}}=

V záznamovém archu uveďte pouze v úloze 3.3 celý postup řešení.

4

4.1 Umocněte a zjednodušte (výsledný výraz nesmí obsahovat závorky):

(0,3x+0,5)2=(0,3x+0,5)^2=

4.2 Rozložte na součin podle vzorce:

49−(−4a)2=49-(-4a)^2=

4.3 Zjednodušte (výsledný výraz nesmí obsahovat závorky):

n⋅(2n−1)−(−2n−n)⋅(3n+2)+(1−2n)⋅(1+2n)=n\cdot(2n-1)-(-2n-n)\cdot(3n+2)+(1-2n)\cdot(1+2n)=

V záznamovém archu uveďte pouze v úloze 4.3 celý postup řešení.

5 Řešte rovnici:

5.1

2−x2+2x=2,5x−3\frac{2-x}{2}+2x=2,5x-3

5.2

3⋅y+12−y3=32⋅2y−33+323\cdot\frac{y+1}{2}-\frac{y}{3}=\frac{3}{2}\cdot\frac{2y-3}{3}+\frac{3}{2}

V záznamovém archu uveďte v obou částech úlohy celý postup řešení (zkoušku nezapisujte).

VÝCHOZÍ TEXT K ÚLOZE 6

V pátek, v sobotu a v neděli se na mýtině vysazovaly stromy.

V sobotu bylo vysázeno o třetinu více stromů než v pátek.
V neděli bylo vysázeno dokonce o 60 % více stromů než v pátek.

(CZVV)

6 Počet stromů vysázených v pátek označíme 𝑝.

6.1 Vyjádřete výrazem s proměnnou 𝑝 počet stromů vysázených v sobotu.

6.2 Vyjádřete výrazem s proměnnou 𝑝 počet stromů vysázených v neděli.

6.3 V pátek bylo vysázeno o 290 stromů méně než v obou zbývajících dnech dohromady.

Vypočtěte, kolik stromů bylo vysázeno v pátek.

VÝCHOZÍ TEXT K ÚLOZE 7

Na parkovišti je přesně 105 parkovacích míst pro osobní auta.
Zaparkuje-li na parkovišti autobus, obsadí vždy 4 parkovací místa pro osobní auta.

(Parkoviště tedy zcela zaplní např. 101 osobních aut a jeden autobus.)

(CZVV)

7

7.1 Na zcela zaplněném parkovišti je počet osobních aut stejný jako počet autobusů.

Vypočtěte, kolik je na parkovišti osobních aut.

7.2 Na zcela zaplněném parkovišti je osobních aut o čtvrtinu více než autobusů.

Vypočtěte, kolik je na parkovišti autobusů.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

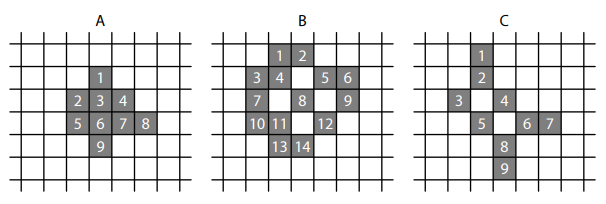
Ve čtvercové síti jsou z tmavých čtverců složeny tři útvary A, B, C.
Z každého útvaru vytvoříme odebráním jediného tmavého čtverce nový útvar, který je osově souměrný podle některé osy (svislé, vodorovné nebo šikmé).

alt text

V jednotlivých útvarech jsme každý tmavý čtverec označili číslem.
Z útvaru A lze vytvořit osově souměrný útvar buď odebráním čtverce 2, nebo odebráním čtverce 8.

(CZVV)

8 Určete číslo čtverce, jehož odebráním vytvoříme osově souměrný útvar

8.1 z útvaru B,

8.2 z útvaru C.

V každé části úlohy najděte obě řešení.

Doporučení pro úlohy 9 a 10: Rýsujte přímo do záznamového archu.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9

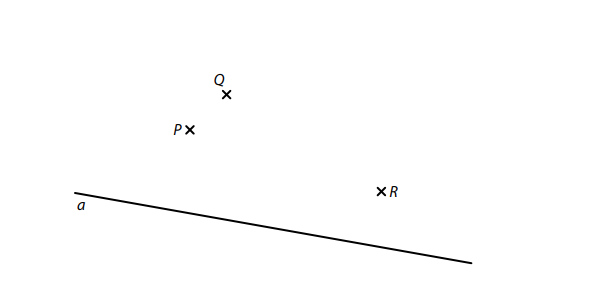
V rovině leží body P, Q, R a přímka a.

alt text

(CZVV)

9

Na přímce a leží strana AB čtverce ABCD.
Dva ze tří bodů P, Q, R leží uvnitř dvou různých stran tohoto čtverce
a třetí bod leží vně čtverce ABCD. Sestrojte všechny vrcholy čtverce ABCD, označte je písmeny a čtverec narýsujte.
Najděte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10

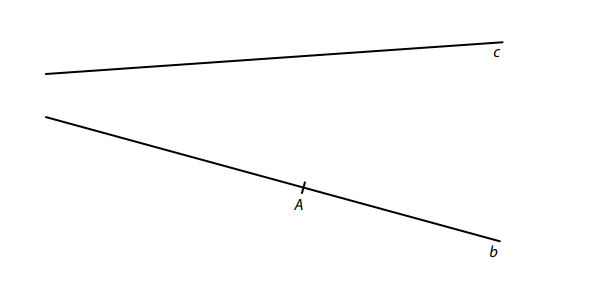
V rovině leží přímky b, c a na přímce b leží bod A.

alt text

(CZVV)

10

Bod A je vrchol trojúhelníku ABC s pravým úhlem při vrcholu A.
Na přímce b leží vrchol B a na přímce c leží vrchol C tohoto trojúhelníku.
Velikost vnitřního úhlu trojúhelníku ABC při vrcholu C je 40°. Sestrojte vrcholy B, C trojúhelníku ABC, označte je písmeny a trojúhelník narýsujte.
Najděte všechna řešení.

V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).

VÝCHOZÍ TEXT A GRAF K ÚLOZE 11

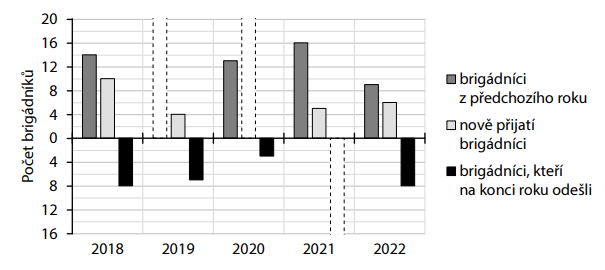
Každý rok pracují v parku jednak brigádníci, kteří tam pracovali v předchozím roce, jednak nově přijatí brigádníci. Na konci každého roku někteří ze všech těchto brigádníků z parku odcházejí a další rok v něm nepracují.

V grafu jsou znázorněny počty brigádníků v letech 2018 až 2022, tři údaje však chybí.

alt text

Např. v roce 2022 pracovalo v parku 9 brigádníků, kteří tam pracovali i v roce 2021, a 6 nově přijatých brigádníků. Z těchto 15 brigádníků jich 8 na konci roku 2022 odešlo.

(CZVV)

11 Rozhodněte o každém z následujících tvrzení (11.1–11.3), zda je pravdivé (A), či nikoli (N).

11.1 V roce 2019 pracovalo v parku 16 brigádníků, kteří tam pracovali i v roce 2018.

11.2 V roce 2020 pracovalo v parku méně než 7 nově přijatých brigádníků.

11.3 Na konci roku 2021 z parku odešlo více než 12 brigádníků.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12

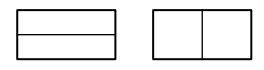
Velký obdélník lze rozdělit na dva shodné menší obdélníky nebo na dva čtverce.

Obvod jednoho z menších obdélníků je 30 cm.

alt text

(CZVV)

12 Jaký je obvod velkého obdélníku?

A)

menší než 36 cm

B)

36 cm

C)

40 cm

D)

60 cm

E)

větší než 60 cm

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

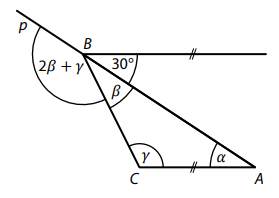
Přímka p prochází vrcholy A, B trojúhelníku ABC, jehož vnitřní úhly mají velikosti 𝛼, 𝛽, 𝛾.

Bodem B prochází rovnoběžka se stranou AC.

alt text

(CZVV)

13 Jaká je velikost úhlu 𝛾?

Velikosti úhlů neměřte, ale vypočtěte.

A)

115°

B)

120°

C)

135°

D)

140°

E)

150°

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

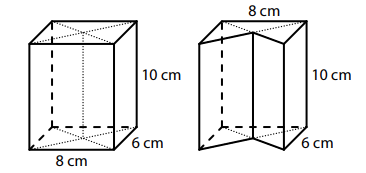
Kvádr s podstavou o rozměrech 6 cm a 8 cm a výškou 10 cm lze dvěma svislými úhlopříčnými řezy rozdělit na čtyři trojboké hranoly s výškou 10 cm.

Odebráním jednoho z trojbokých hranolů vznikne z kvádru pětiboký hranol jako na obrázku vpravo.

alt text

(CZVV)

14 O kolik cm2 se liší povrch pětibokého hranolu a povrch původního kvádru?

A)

o 4 cm2

B)

o 16 cm2

C)

o 24 cm2

D)

o 30 cm2

E)

o jiný počet cm2

15 Přiřaďte ke každé úloze (15.1–15.3) odpovídající výsledek (A–F).

15.1 Letos se na gymnázium přihlásilo 420 uchazečů, což je o 40 % více, než se jich přihlásilo loni.

Kolik uchazečů se na gymnázium přihlásilo loni?

15.2 On-line kurzu českého jazyka se zúčastnilo 180 žáků, což je o 25 % méně, než se jich zúčastnilo on-line kurzu matematiky.

Kolik žáků se zúčastnilo on-line kurzu matematiky?

15.3 Včera navštívilo plavecký bazén celkem 680 dospělých, mezi nimiž bylo mužů o 30 % méně než žen.

Kolik mužů včera navštívilo plavecký bazén?

A)

méně než 240

B)

240

C)

260

D)

280

E)

300

F)

více než 300

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16

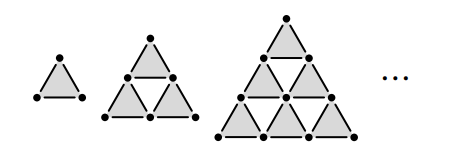
Obrazce tvaru trojúhelníku se sestavují skládáním šedých trojúhelníků do pater (viz obrázek).

Šedé trojúhelníky mají ve vrcholech puntíky a na stranách stejně dlouhé úsečky. V prvním obrazci je pouze jeden šedý trojúhelník a každý další obrazec má o jedno patro šedých trojúhelníků více než předchozí obrazec.

alt text
Patra 1 2 3
Šedé trojúhelníky 1 3 6
Puntíky 3 6 10
Úsečky 3 9 18

(CZVV)

16

16.1 Určete počet úseček v obrazci, který má 5 pater.

16.2 Počet úseček v posledním a v předposledním obrazci se liší o 96.

Určete, o kolik se liší počet puntíků v posledním a předposledním obrazci.

16.3 V jednom obrazci je 300 puntíků.

Určete počet úseček v následujícím obrazci.