1 Adam a Naďa šli spolu z Heraltic do Hvězdoňovic trasou dlouhou 2,7 km. Adam má délku každého kroku 75 cm, Naďa má každý krok dlouhý 60 cm.
O kolik kroků udělala Naďa více?
2 Reproduktory byly před Vánocemi zlevněny z původní ceny o 150 korun, což bylo 15 % původní ceny. Po Vánocích je prodejce zlevnil ještě o 200 korun z nové ceny.
O kolik procent byla konečná cena nižší než cena původní?
3 Vypočítejte a výsledek zapište zlomkem v základním tvaru.
Do záznamového archu uveďte u obou podúloh celý postup řešení.
3.1
3.2
4
4.1 Upravte a rozložte na součin vytknutím:
4.2 Umocněte a zjednodušte:
4.3 Upravte výraz tak, aby neobsahoval závorky, a zjednodušte:
Do záznamového archu uveďte u podúlohy 4.3 celý postup řešení.
5 Řešte rovnice.
Do záznamového archu uveďte u obou podúloh celý postup řešení. Zkoušku nezapisujte.
5.1
5.2
6 Ve vnitrostátním rychlíku jsou řazeny vagóny 1. a 2. třídy. Vagónů 2. třídy je dvakrát více než vagónů 1. třídy. V každém vagónu je 10 kupé (oddílů pro cestující). Ve vagónech 1. třídy je v každém kupé šest míst k sezení, ve vagónech 2. třídy osm míst k sezení. Ve všech kupé rychlíku je dohromady 440 míst k sezení.
6.1 Kolik vagónů 2. třídy je součástí rychlíku?
6.2 Kolik míst k sezení je dohromady ve vagónech 1. třídy?
VÝCHOZÍ TEXT A TABULKA K ÚLOZE 7
V restauraci nabízejí tři různá obědová menu (polévku, hlavní jídlo a nápoj) označená písmeny A, B a C. Do restaurace přijely tři skupiny turistů po dvaceti lidech. V tabulce jsou uvedeny obědy, které si jednotlivé skupiny objednaly, a kolik za ně zaplatily.
Počet obědů Počet obědů Počet obědů Celková cena za obědy A B C skupina 1 20 0 0 4 000 Kč skupina 2 10 10 0 4 800 Kč skupina 3 5 5 10 5 400 Kč
7
7.1 Jaká byla cena oběda B?
7.2 Jaká byla cena oběda C?
VÝCHOZÍ TEXT A GRAFY K ÚLOZE 8
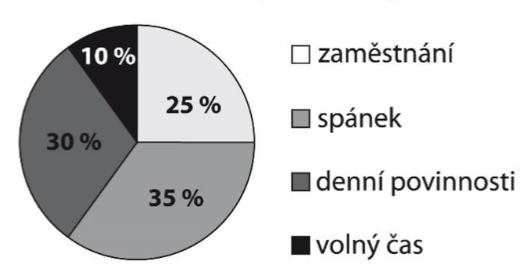
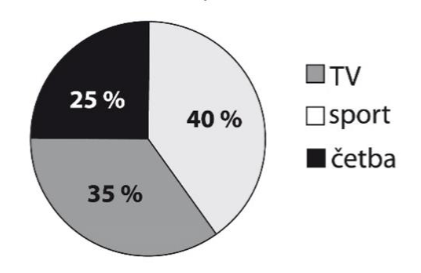
V prvním grafu je uvedeno průměrné časové rozložení všech denních činností paní Kratochvílové v pracovní den. Ve druhém grafu je zaznamenáno rozložení jejího volného času v pracovní den.
Denní činnosti (24 hodin)
Volný čas
8 Vypočítejte:
8.1 Kolik hodin denně paní Kratochvílová tráví v zaměstnání?
8.2 Kolik minut denně paní Kratochvílová sportuje?
Výsledek zaokrouhlete na celé minuty.
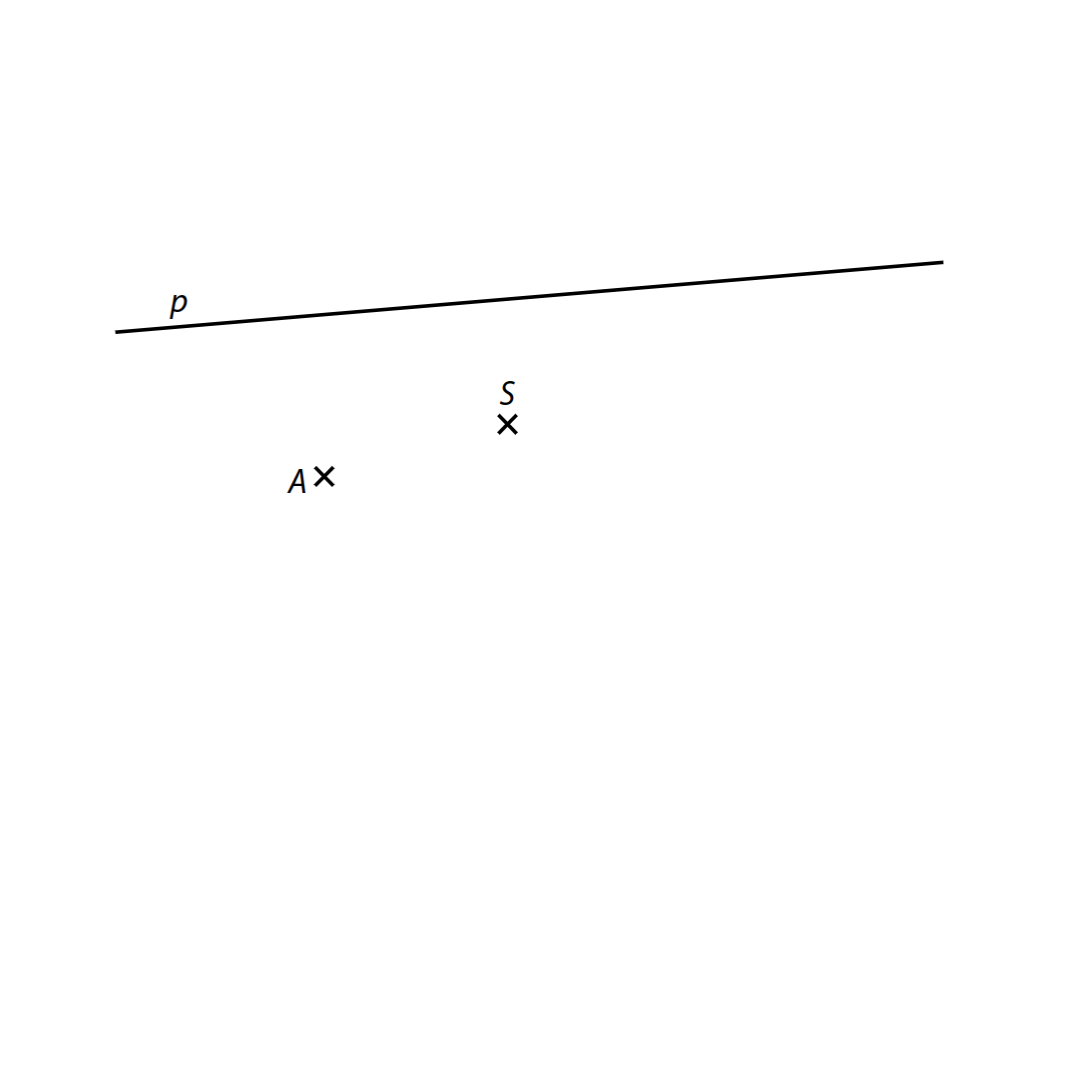
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9
V rovině je dána přímka p a body A a S, které neleží na přímce p. Bod A je vrchol obdélníku ABCD, bod S je střed obdélníku (průsečík úhlopříček). Vrchol D obdélníku leží na přímce p.
9 Sestrojte obdélník ABCD.
Nalezněte všechna řešení.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).
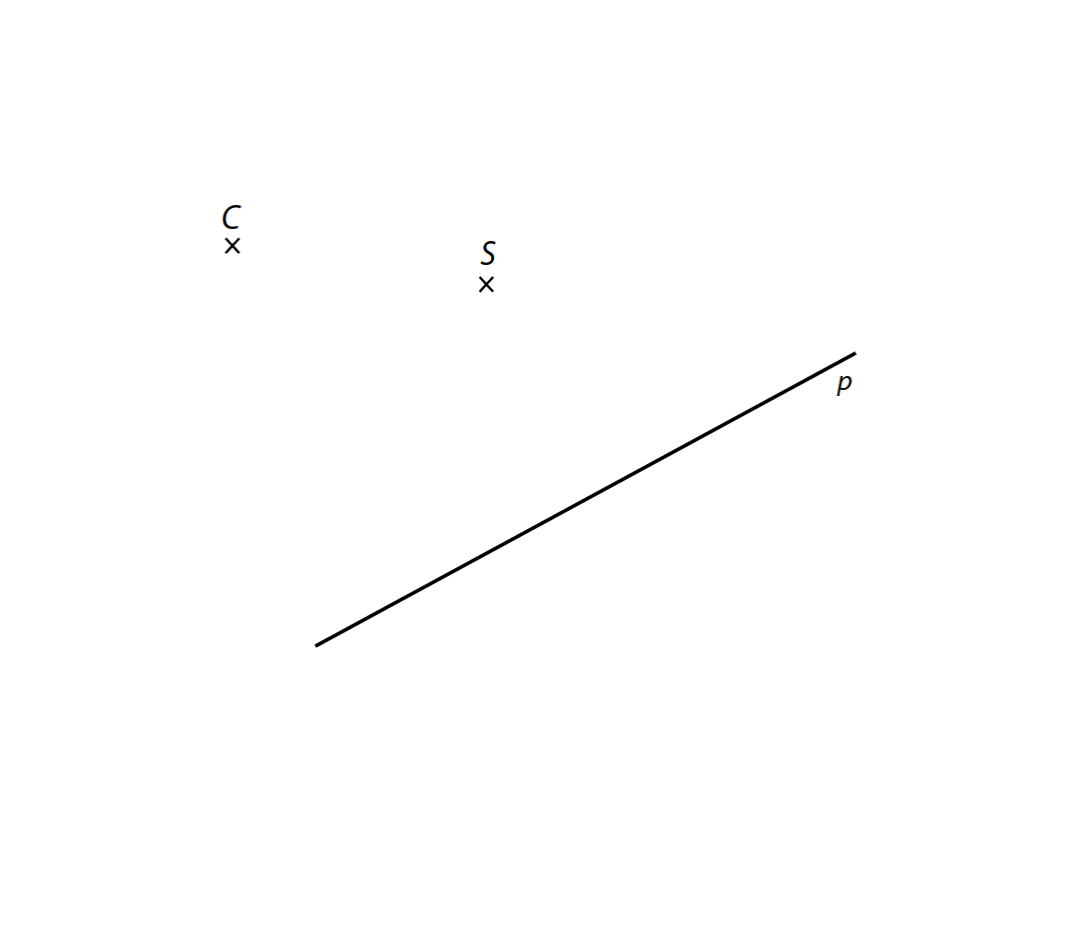
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10
V rovině leží body C, S a přímka p. Bod C je vrchol pravoúhlého trojúhelníku ABC.
Bod S je střed strany BC tohoto trojúhelníku. Strana AB tohoto trojúhelníku je rovnoběžná s přímkou p.
10 Sestrojte pravoúhlý trojúhelník ABC.
Najděte všechna řešení.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (všechny čáry, kružnice nebo jejich části i písmena).
11 V obchodě prodávají dámská a pánská trička. Ráno před začátkem otevírací doby tvořila dámská trička 60 % z celkového naskladněného množství triček, zbytek byla trička pánská. Přes den se prodalo 45 dámských triček, což je čtvrtina všech dámských triček, která byla v obchodě naskladněna ten den ráno. Pánských triček se ze všech naskladněných pánských triček prodala polovina.
Kolik zůstalo na konci dne v obchodě triček (dámských i pánských dohromady)?
méně než 200
200
210
220
více než 220
12 Petr přečetl již 1 050 stran knižní série, do konce mu zbývá přečíst ještě 450 stran.
Kolik procent stran knižní série Petrovi zbývá dočíst?
27 %
30 %
33 %
40 %
43 %
13 Maminka oškrabe 6 kg brambor za 2 hodiny a 24 minut. Babička oškrabe 2 kg brambor za 1 hodinu a 20 minut. Maminka i babička škrabou brambory stálým tempem.
Za kolik minut oškrabou maminka a babička 1 kg brambor, pokud škrabou obě dohromady?
za 64 minut
za 32 minut
za 15 minut
za 12 minut
jiný výsledek
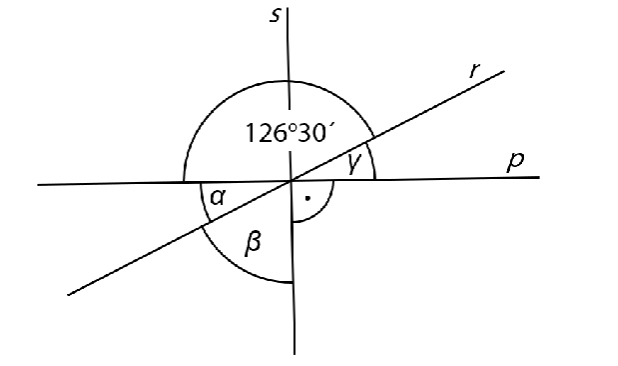
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14
Přímky p, r a s se protínají v jednom bodě.
14 Jaký je součet úhlů α + β + γ?
Velikosti úhlů neměřte, ale vypočítejte (obrázek je ilustrační).
126° 30´
133° 30´
143° 30´
180°
jiný výsledek
15 V obchodě mají dva druhy jablek. Kilogram jednoho druhu (dražších) jablek stojí 30 Kč, kilogram druhého druhu (levnějších) jablek stojí 25 Kč. Paní Vitamínová koupila x kilogramů jablek, kde x je celé číslo, a zaplatila 330 Kč.
Rozhodněte o každém z následujících tvrzení (15.1–15.3), zda je pravdivé (A), či nikoli (N).
15.1 Pokud paní Vitamínová koupila 12 kg jablek, koupila stejná množství obou druhů jablek.
15.2 Paní Vitamínová mohla koupit jen levnější druh jablek.
15.3 Pokud chce paní Vitamínová koupit co nejvíce kilogramů jablek, musí koupit právě jeden kilogram drahých jablek.
16 Přiřaďte ke každé podúloze (16.1–16.3) odpovídající výsledek (A–F).
16.1 Zvětšíme-li neznámé číslo o 4 %, dostaneme číslo 780.
Jaké je toto neznámé číslo?
16.2 O kolik procent musíme zvětšit , abychom dostali ?
16.3 Máme dvě čerpadla. Jejich výkony jsou v poměru 3:7. Méně výkonné čerpadlo vyčerpá 150 litrů vody za dvě hodiny. Kolik litrů vody vyčerpá výkonnější čerpadlo za 5 hodin?
300
400
720
750
875
jiný výsledek