1 Vypočtěte, o kolik cm2 je plocha o obashu 0,2 m2 větší než plocha o obsahu 20 cm2.
2 Vypočítejte:
2.1
2.2
3 Vypočítejte a výsledek zapište zlomkem v základním tvaru.
Do záznamového archu uveďte u obou podúloh celý postupu řešení.
3.1
3.2
4
4.1 Zjednodušte (výsledný výraz nesmí obsahovat závorky):
4.2 Rozložte na součin podle vzorce:
4.3 Zjednodušte a výsledek rozložte na součin vytýkáním:
5 Řešte soustavu rovnic.
Do záznamového archu uveďte u obou podúloh celý postupu řešení.
Zkoušku nazapisujte.
5.1
5.2
VÝCHOZÍ TEXT K ÚLOZE 6
Zahradník sázel na záhon sazenice. Sazenice salátů zasadil o 4 více než sazenic okurek.
Na záhoně čtvrtinu sazenic salátů zlikvidovali slimáci a šestina sazenic okurek uschla.
Všechny ostatní sazenice se ujaly. Na záhoně se tak ujal stejný počet sazenic salátů a okurek.
6 Určete,
6.1
kolik sazenic salátů zahradník zasadil,
6.2
kolik sazenic okurek se ujalo.
VÝCHOZÍ TEXT K ÚLOZE 7
Stejné výrobky jsou po 12 kusech baleny do stejných krabic.
Na váhu se položily tři krabice, z nichž dvě byly plné, ale ve třetí krabici 5 výrobků chybělo.
Tyto tři krabice i s výrobky vážily dohromady 2 kg.Když se z váhy odebraly obě plné krabice, display váhy ukazoval 480g.
7 Vypočtěte, jaká je hmotnost v gramech
7.1 jedné plné krabice,
7.2 jednoho výrobku,
7.3 jedné prázdné krabice.
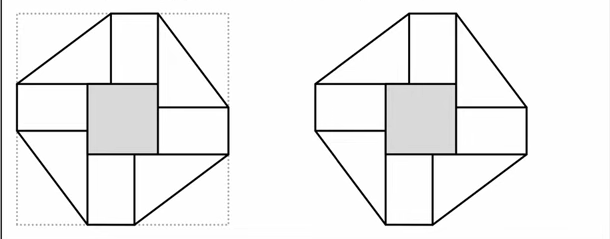
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8
Z rohů čtverce se stranou délky 27 cm se nejprve odstřihnou čtyři shodné trojúhelníky a poté se vykreslí ornament.
Ornament obsahuje jeden tmavý čtyřúhelník uprostřed, čtyři shodné bílé obdélníky a čtyři shodné bílé trojúhelníky, jejichž kratší strany mají délky 9 cm a 12 cm.
8 Vypočtěte
8.1 v cm obvod ornamentu (zakresleného vpravo),
8.2 v cm2 celkový obsah bílých ploch ornamentu (zakresleného vpravo),
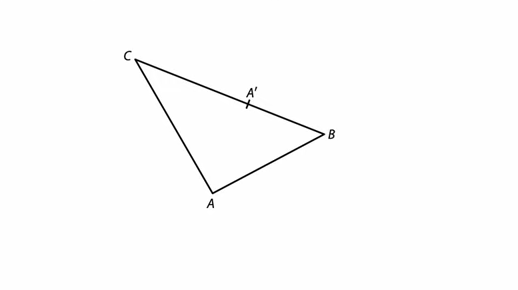
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 9
V rovině leží trojúhelník ABC, na jehož straně BC je umístěn bod A'.
9 Bod A' je vrchol trojúhelníku A'B'C', který je obrazem trojúhelníku ABC ve středové souměrnosti se středem S.
Sestrojte a označte písmenem střed souměrnosti S. Sestrojte vrcholy B' a C' trojúhleníku A'B'C', označte je písmeny a trojúhelník narýsujte.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).
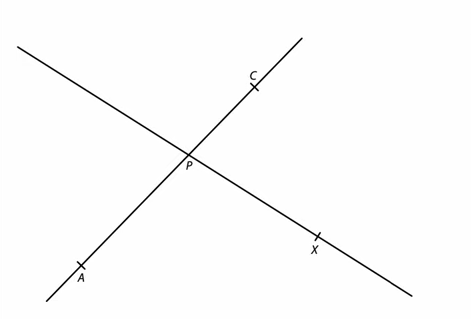
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 10
V rovině leží přímka AC a PX, které se protínají v bodě P.
10
Body A, C jsou vrcholy pravoúhlého lichoběžníku ABCD se základnami AB, CD a pravým úhlem při vrcholu D. Bod P je průsečík úhlopříček tohoto lichoběžníku. Vrchol D leží na přímce PX.
Sestrojte vrcholy B,D pravoúhlého lichoběžníku ABCD, označte je písmeny a lichoběžník narýsujte.
Najděte všechna řešení.
V záznamovém archu obtáhněte celou konstrukci propisovací tužkou (čáry i písmena).
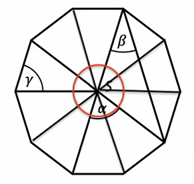
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11
V náčrtku pravidelného desitiúhelníku se středem S jsou vyznačeny úhly , , .
11 Rozhodněte o každém z následujících tvrzení (11.1-11.3), zda je pravdivé (A), či nikoli (N).
Úhly neměřte, náčrtek není přesný.
11.1
11.2
11.3
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 12
Kytice byla svázána ze tří druhů květin: růží, chryzantém a static.
Růží a chryzantém dohromady je v kytici o 2 více než chryzantém a static dohromady. Počet růží ku počtu static je v poměru 5 : 4, počet static ku počtu chryzantémm v poměru 2 : 3.
V tabulce je u každého druhu květin uvedena cena za jeden kus. Cena celé kytice se získá jako součet cen jednotlivých květin, z nichž byla kytice svázána.
Druh květiny Cena za kus Počet kusů v kytici Růže 54 korun Chryzantéma 40 korun Statice 35 korun
12 Kolik korun bude stát celá kytice?
1090 korun
1252 korun
1280 korun
1300 korun
jinou částku
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13
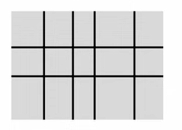
Na čtvrtku papíru narýsujeme rovné čáry, které jsou rovnoběžné s jedním nebo s druhým okrajem čtvrty. Čáry jsou nakresleny přes celou čtvrtku a rozdělují ji na několik částí.
Např. na obrázku rozděluje 6 rovných čar čtvrtku na 15 částí.
13 Jaký je nejmenší počet rovných čar, které rozdělí čtvrtku na 40 částí?
11
12
13
14
větší než 14
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14
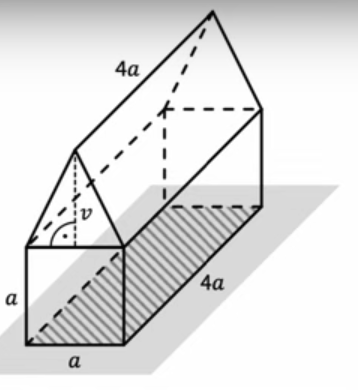
Dřevěný domeček se skládá ze dvou kolmých hranolů a stojí na vodorovné podložce.
Plocha, kterou se domeček dotýká podložky, má obsah 16 cm2.
V obrázku jsou označeny některé rozměry hranolů. Platí v = a.
14 Jaký je objem domečku?
42 cm3
48 cm3
56 cm3
64 cm3
jiný objem
15 Přiřaďte ke každé úloze (15.1-15.3) odpovídající výsledek (A-F).
15.1 Tři pětiny objemu nádoby jsou zaplněny vodou. Celou nádobu zaplníme po dolití dalších 14 litrů vody. (Nádoba nepřeteče.)
Jaký je objem nádoby?
15.2 Voda v v nádobě vyplňuje 55 % jejího objemu. Když z nádoby odebereme 12 litrů vody, bude zaplněna přesně čtvrtina objemu nádoby.
Jaký je objem nádoby?
15.3
V každé ze tří stejných nádob je nalito jíné množství vody. V první nádobě vyplňuje voda 30 % jejího objemu a ve druhé nádobě 40 % objemu. Ve třetí nádobě je 19 litrů vody. Kdybychom vodu ze všech nádob rozdělili rovnoměrně, voda by v každé nádobě vyplnila dvě pětiny jejího objemu.
Jaký je objem jedné nádoby?
30 litrů
33 litrů
35 litrů
38 litrů
40 litrů
jiný objem
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 16
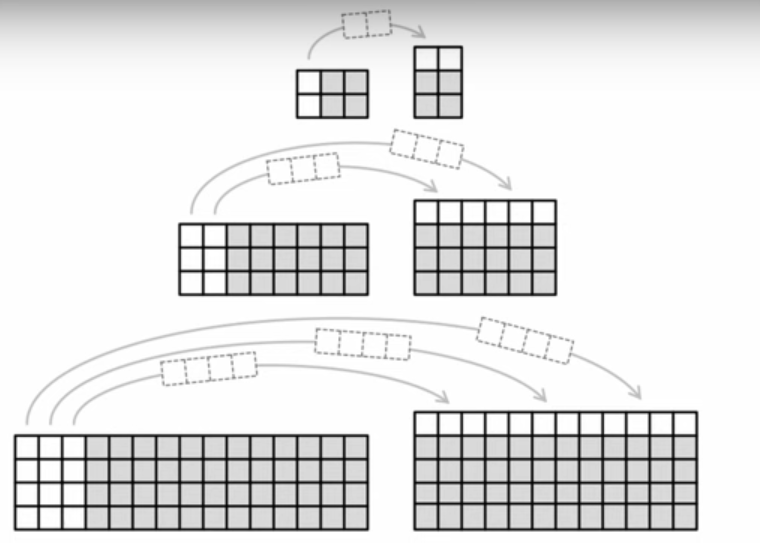
Pro každou dvojici obdélníků sestavených ze stejného počtu čtverečků platí:
- Vyšší z obou obdélníků má vždy o jednu řadu čtverečků více než nižší obdélník.
- Vyšší obdélník vznikne z nižšího obdélníku přesunutím několika sloupců do horní řady.
- Počet přesunutých sloupců je vždy o 1 menší, než je počet řad v nižším obdélníku. Tedy z obdélníku se 2 řadami se přemístí 1 sloupec, z obdélníku se 3 řadami 2 sloupce, atd.
16
16.1
V jedné dvojici obdélníků má nižší obdélník 21 řad. V této dvojici určete počet sloupců ve vyšším obdélníku.
16.2
V jiné dvojici obdélníků má vyšší obdélník 110 sloupců. V této dvojici určete počet řad v nižším obdélníku.