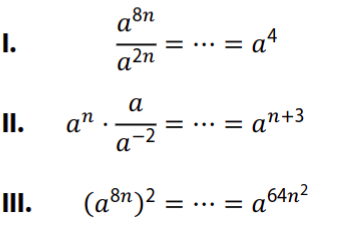VÝCHOZÍ TEXT K ÚLOZE 1

Firma utržila v únoru pouze čtyři pětiny toho, co utržila v lednu.

(CZVV)

1 Určete, o kolik procent více utržila firma v lednu než v únoru.

VÝCHOZÍ TEXT K ÚLOZE 2

Je dán čtverec o straně délky a. Obdélník o obsahu 360 cm2 má jednu stranu o 8 cm delší než daný čtverec a druhou stranu o 8 cm kratší než daný čtverec.

(CZVV)

2 Vypočtěte v cm2 obsah daného čtverce.

Výsledek ani dílčí výpočty nezaokrouhlujte.

3 Pro x∈R{−2;0;2}{x \in R \{-2;0;2\}} zjednodušte:

1x+2−x2x2−4x2=\frac{1}{x + 2} - \frac{\frac{x^2}{x^2 - 4}}{\frac{x}{2}} =

V záznamovém archu uveďte celý postup řešení.

4 V oboru R řešte:

x+5x+1+5x−1x2−x=5x\frac{x+5}{x+1} + \frac{5x-1}{x^2 - x} = \frac{5}{x}

V záznamovém archu uveďte celý postup řešení.

5 Pro x∈R{x \in R}, y∈R{y \in R} řešte soustavu rovnic:

x+2y=5x2=10−4y\begin{aligned} x+2y &= 5\\ \frac{x}{2} &= 10 - 4y \end{aligned}

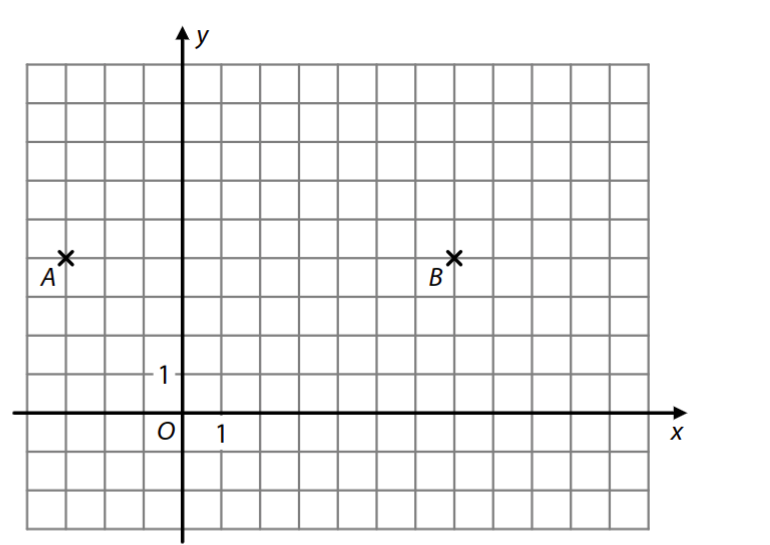
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 6

V kartézské soustavě souřadnic Oxy jsou vyznačeny dva mřížové body A, B. Jejich vzdálenost je dvojnásobkem vzdálenosti bodu B od bodu K [7;k], kde k∈R.

alt text
(CZVV)

6 Určete souřadnici k.

Uveďte všechna řešení.

7 Je dán výraz:

log⁡2(8−x){ \log_2(8^{-x})}

Určete všechna x∈Rx \in R, pro která je hodnota daného výrazu rovna osmi.

V záznamovém archu uveďte celý postup řešení.

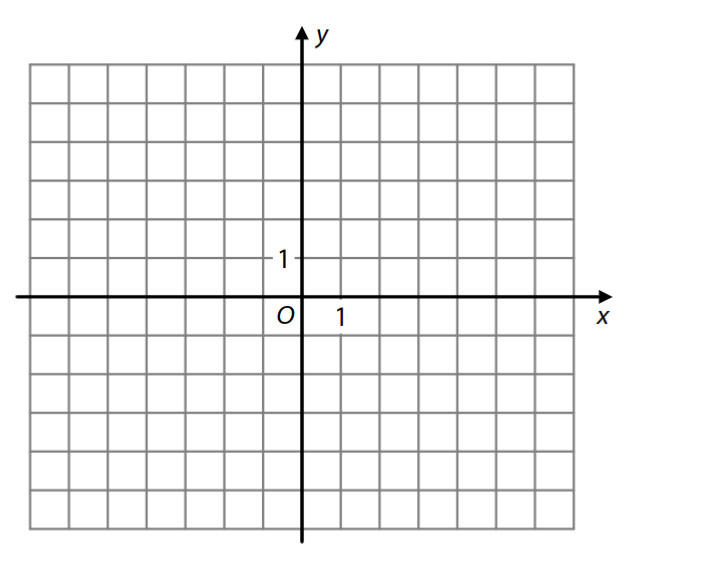
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8

Grafem funkce h:y=3x−2−4h:y= \frac{3}{x- 2}-4 je hyperbola se středem S (bod S je průsečík asymptot). Graf lineární funkce f prochází bodem R[-5;1] a bodem S.

alt text

(CZVV)

8

8.1 Určete obě souřadnice středu S.

8.2 V kartézské soustavě souřadnic Oxy sestrojte graf lineární funkce f.

V záznamovém archu obtáhněte vše propisovací tužkou.

VÝCHOZÍ TEXT K ÚLOHÁM 9–10

Pro x∈R{ x \in R} je dána funkce:

g:y=sin(x+7π6){ g:y = sin (x + \frac{7\pi}{6})}

(CZVV)

9 Vypočtěte obě souřadnice průsečíku P grafu funkce 𝑔 se souřadnicovou osou y.

10 Určete nejmenší kladné číslo x, pro které platí:

sin(x+7π6)=1{ sin(x + \frac{7\pi}{6}) = 1}

VÝCHOZÍ TEXT A GRAF K ÚLOHÁM 11–12

Do třídy 6. A chodí 25 žáků.
Každý z nich uvedl počet hudebních nástrojů, na které hraje.
V grafu četností hodnot tohoto znaku právě dvě četnosti chybí (počet žáků, kteří nehrají na žádný hudební nástroj, a počet žáků, kteří hrají pouze na jeden hudební nástroj). Chybějící četnosti se vzájemně liší o 10.
Modus počtu hudebních nástrojů je 0.

alt text (CZVV)

11 Určete medián počtu hudebních nástrojů, na které hraje žák třídy 6. A.

12 Určete aritmetický průměr počtu hudebních nástrojů, na které hraje žák třídy 6. A.

Výsledek nezaokrouhlujte.

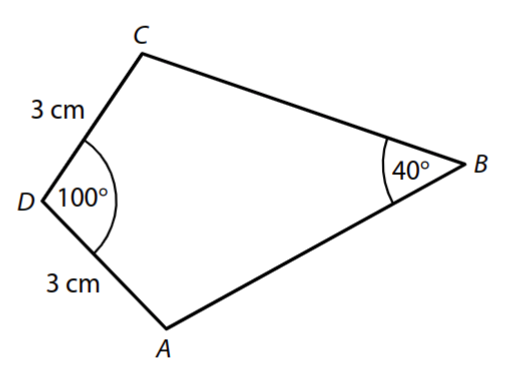
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

Čtyřúhelník ABCD se skládá ze dvou shodných trojúhelníků ABD a CBD. Platí: |AD|=|CD|=3 cm, |∢ADC|=100°, |∢ABC|=40°.

alt text

(CZVV)

13 Vypočtěte v cm délku úhlopříčky

13.1 AC,

13.2 BD.

Výsledky zaokrouhlete na desetiny cm. V záznamovém archu uveďte v obou částech úlohy celý postup řešení.

VÝCHOZÍ TEXT K ÚLOZE 14

Pro třídenní propagační akci byly vydány poukazy na jeden volný vstup do aquacentra. První den akce byly využity dvě pětiny všech vydaných poukazů.
Každý další den akce bylo využito o 15 poukazů méně než v předchozím dni. Během celé třídenní akce nebyla využita pouze jedna dvacetina všech vydaných poukazů. (CZVV)

14 Užitím rovnice nebo soustavy rovnic vypočtěte, kolik vydaných poukazů bylo využito druhý den propagační akce.

V záznamovém archu uveďte celý postup řešení (popis neznámých, sestavení rovnice, resp. soustavy rovnic, řešení a odpověď ).

VÝCHOZÍ TEXT K ÚLOZE 15

V kartézské soustavě souřadnic Oxy je dána přímka

p:x=2+2𝑡,y=1−4𝑡,t∈R{ p:x=2+2𝑡, y=1-4𝑡, t \in R }

(CZVV)

15 Rozhodněte o každém z následujících tvrzení (15.1–15.3), zda je pravdivé (A), či nikoli (N).

15.1 Přímka p prochází bodem M[3;-1].

15.2 Vektor u⃗=(2;1){ \vec{u} = (2;1)} je směrovým vektorem přímky p.

15.3 Přímka p je kolmá k přímce q:2𝑥+𝑦=0{ q:2𝑥+𝑦=0}.

VÝCHOZÍ TEXT K ÚLOZE 16

Rada sportovního klubu má 11 členů, z nichž právě tři obsadí funkce předsedy, místopředsedy a hospodáře. Kandidaturu na funkci předsedy i na funkci místopředsedy přijalo všech 11 členů rady, ale pouze 6 z nich přijalo i kandidaturu na funkci hospodáře.

(CZVV)

16 Kolika způsoby lze všechny tři funkce obsadit?

A)

440 způsoby

B)

540 způsoby

C)

660 způsoby

D)

1 440 způsoby

E)

jiným počtem způsobů

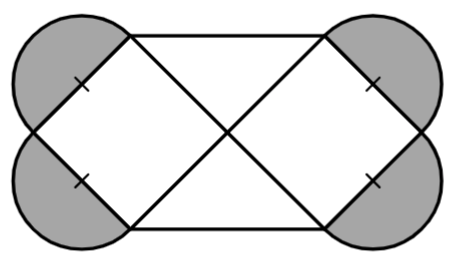
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 17

Obrazec obsahuje čtyři tmavé půlkruhy a bílý šestiúhelník, který se skládá ze dvou shodných čtverců a dvou shodných rovnoramenných trojúhelníků. Celkový obsah tmavých částí obrazce je 32π cm2.

(Průměrem každého půlkruhu je strana čtverce.) alt text

(CZVV)

17 Jaký je obsah bílého šestiúhelníku?

A)

48 cm2

B)

96 cm2

C)

128 cm2

D)

183 cm2

E)

192 cm2

VÝCHOZÍ TEXT K ÚLOZE 18

Vnitřní prostor konvičky na mléko má tvar rotačního válce s podstavou o průměru 6 cm. Vnitřní prostor kalíšku, který je zcela zaplněn mlékem do kávy, má tvar rotačního válce s podstavou o průměru 2,4 cm a výškou 1,5 cm. Všechno mléko z kalíšku jsme přilili do konvičky s mlékem.

(Konvička nebyla nakloněna, mléko nepřeteklo.)

(CZVV)

18 O kolik stoupla hladina v konvičce po přilití mléka z kalíšku?

A)

o méně než 0,24 cm

B)

o 0,24 cm

C)

o 0,68 cm

D)

o 0,72 cm

E)

o více než 0,72 cm

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 19

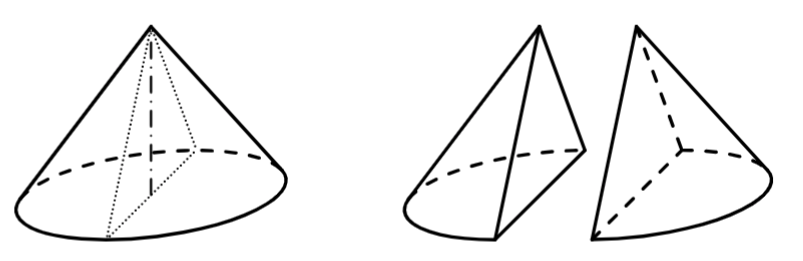
Dřevěný rotační kužel s podstavou o poloměru 12 cm a výškou 16 cm jsme osovým řezem rozdělili na dva shodné půlkužele.

alt text

(CZVV)

19 Jaký je povrch jednoho půlkužele?

Výsledek je zaokrouhlen na celé cm2.

A)

603 cm2

B)

720 cm2

C)

795 cm2

D)

1 206 cm2

E)

jiný povrch

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 20

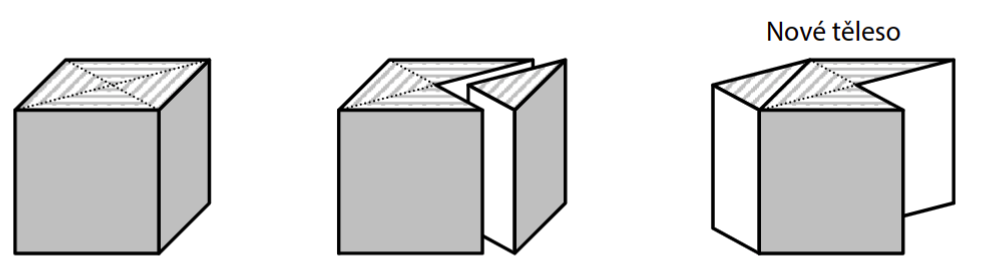
Z krychle s hranou délky 4 cm byl dvěma úhlopříčnými svislými řezy oddělen trojboký hranol, který tvoří čtvrtinu krychle. Oddělený hranol se přemístil tak, aby jeho čtvercová stěna splynula s protější stěnou krychle. Vzniklo tak nové těleso.

alt text

(CZVV)

20 Jaký je povrch nového tělesa?

Výsledek je zaokrouhlen na celé cm2.

A)

109 cm2

B)

128 cm2

C)

135 cm2

D)

155 cm2

E)

jiný povrch

21 Pro kterou z následujících nerovnic je množinou všech řešení v oboru R interval (7;+∞)(7;+\infty) ?

A)

7−x>0{7-x > 0}

B)

(x−7)2>0{(x-7)^2 > 0}

C)

x2−49>0{ x^2 - 49 > 0}

D)

(x−1)2x−7>0{\frac{(x-1)^2}{x -7} > 0}

E)

x−7x−1>0{\frac{x-7}{x-1} > 0}

VÝCHOZÍ TEXT K ÚLOZE 22

Jsou uvedeny úpravy tří výrazů:

alt text

(CZVV)

22 Který výraz byl upraven správně pro každé a∈(0;+∞){a \in (0;+\infty)} a každé n∈N{ n \in N} ?

A)

Správně byly upraveny alespoň dva ze tří výrazů.

B)

pouze I.

C)

pouze II.

D)

pouze III.

E)

Správně nebyl upraven žádný ze tří výrazů.

VÝCHOZÍ TEXT K ÚLOZE 23

V osudí je 6 černých míčků a 4 bílé míčky. Náhodně vytáhneme dvojici míčků.

(CZVV)

23 Jaká je pravděpodobnost, že oba dva vytažené míčky budou mít stejnou barvu?

A)

715\frac{7}{15}

B)

15\frac{1}{5}

C)

12\frac{1}{2}

D)

23\frac{2}{3}

E)

jiná hodnota pravděpodobnosti

VÝCHOZÍ TEXT K ÚLOZE 24

Firma svým britským pracovníkům poskytla příplatek na bydlení 1,2 libry na čtvereční yard. Českým pracovníkům firma poskytla odpovídající příplatek v korunách na čtvereční metr, a to s využitím následujících převodů:

1 £=29,6 Kč

1 yd=91,44 cm

(CZVV)

24 V jaké výši poskytla firma příplatek na bydlení českým pracovníkům?

Přesně vypočtená hodnota je zaokrouhlena na desetiny.

A)

29,7 Kč na 1 m2

B)

30,9 Kč na 1 m2

C)

32,4 Kč na 1 m2

D)

38,8 Kč na 1 m2

E)

42,5 Kč na 1 m2

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 25

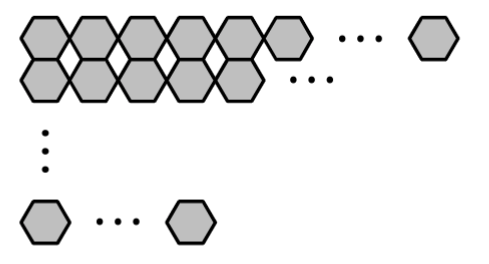
Dvě různé mozaiky jsou sestaveny z několika řad shodných šestiúhelníků.

alt text

25.1

První mozaika obsahuje 10 řad.
Nejvíce šestiúhelníků je v horní řadě. V každé další řadě je o polovinu méně šestiúhelníků než v řadě nad ní.
Ve třetí řadě zdola je 36 šestiúhelníků.

25.2

Druhá mozaika obsahuje lichý počet řad.
Nejvíce šestiúhelníků je v horní řadě. V každé další řadě je o 15 šestiúhelníků méně než v řadě nad ní. Nejméně šestiúhelníků je tedy ve spodní řadě.
V prostřední řadě je 260 šestiúhelníků a ve spodní řadě 140 šestiúhelníků.

(CZVV)

25 Ke každé otázce (25.1–25.2) přiřaďte správnou odpověď (A–F).

25.1 Kolik šestiúhelníků je v horní řadě první mozaiky?

25.2 Kolik šestiúhelníků dohromady obsahuje druhá mozaika?

A)

méně než 4 000

B)

4 096

C)

4 420

D)

4 608

E)

4 680

F)

více než 4 700